平面最近点对(加强版)¶
题目背景¶
P7883 平面最近点对(加强加强版)
题目描述¶
给定平面上 \(n\) 个点,找出其中的一对点的距离,使得在这 \(n\) 个点的所有点对中,该距离为所有点对中最小的
输入格式¶
第一行:\(n\) ,保证 \(2\le n\le 200000\) 。
接下来 \(n\) 行:每行两个实数:\(x\ y\) ,表示一个点的行坐标和列坐标,中间用一个空格隔开。
输出格式¶
仅一行,一个实数,表示最短距离,精确到小数点后面 \(4\) 位。
样例 #1¶
样例输入 #1¶
3
1 1
1 2
2 2
样例输出 #1¶
1.0000
提示¶
数据保证 \(0\le x,y\le 10^9\)
solu¶
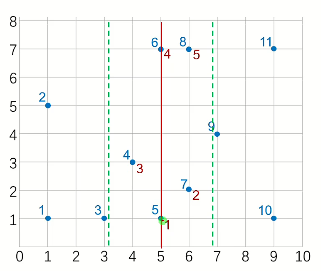
模拟以下算法
先不断往下分,一直分到[1,2]和[3,3]
发现1,2是相邻点,1直接返回距离差,d→4
发现3,3是同一个点,距离无限→无限,的不变
接下来跨中线处理(在线上的看作属于左边),发现1,3比1,2近,d→2
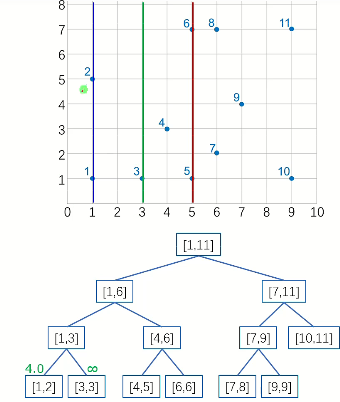
分完[1,3]再分[4,6]
4,5同上,d→2
6,6同上,d不变
跨中线(图中斜线)处理,发现4,6距离>d,不管
返回到[1,6],左右边的d最小值都已经处理好了,[1,3]为2.0,[4,6]为2.2
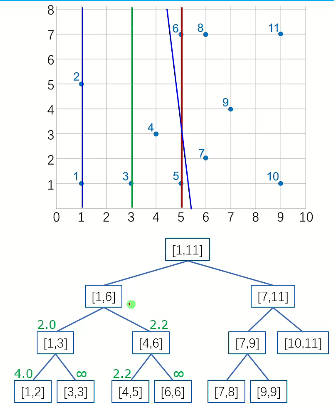
接下来跨中线处理(绿线)发现3,5距离和左边的d相同,不更新
但跨中线处理还是必要的!
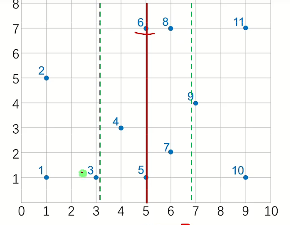
在[7,9]和[1,11]中,d最小值都是由跨中线的情况得来的
本题重点
-
跨中线点的距离计算
-
分治思路
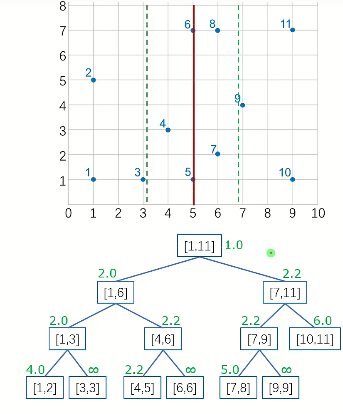
我们来详细看一下跨中线的算法
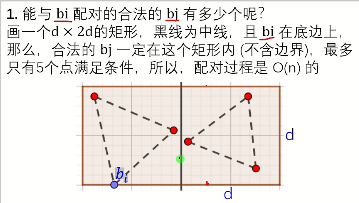
当计算到跨中线时,左右两边的d的最小值 \(d_l,d_r\) 已经计算出来了
这时候计算 \(d_l,d_r\) 的最小值为 \(d_{min}\),将离中线水平距离≤d_{min}的点处理出来(即图中绿虚线范围内的点)
因为目前要找的是跨中线的两点间距离d,如果有一边的点到中线水平距离就>d_{min}的话,取d_{min}最优,就不需要考虑了,将这些点处理掉,等下直接跳过
补充知识
函数 double fabs (double x) 返回浮点数 x 的绝对值。. 注意: fabs () 函数可以用于 double、float 和 long double 类型的参数。. 如果需要计算整数的绝对值,应该使用 abs ()
复杂度分析


code 28 TLE¶
/*////////ACACACACACACAC///////////
. Code by Ntsc .
. Love by Liye .
/*////////ACACACACACACAC///////////
#include<bits/stdc++.h>
#define ll long long
#define db double
#define rtn return
#define i1n int i=1;i<=n;i++
#define in1 int i=n;i>=1;i--
using namespace std;
const int N=2e5+5;
const int M=1e5;
const int Mod=1e5;
const int INF=1e5;
int n,ans;
struct node{
db x,y;
}a[N],b[N];
bool cmp(node a,node b){
return a.x<b.x;
}
bool cmpy(node a,node b){
return a.y<b.y;
}
db dis(node a,node b){
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
db solve(int l,int r){
if(l==r)return 2e9;//l和r是同一个点,不处理
if(l==r-1)return dis(a[l],a[r]); //l,r两点相邻
//分裂
int mid=(l+r)/2;
db d=min(solve(l,mid),solve(mid+1,r));
//跨中线寻找更优解
int k=0;
for(int i=1;i<=r;i++){
if(fabs(a[i].x-a[mid].x)<d)b[++k]=a[i];//找出绿虚线范围内的点,加入数组b[]
}
sort(b+1,b+k+1,cmpy);//按y排序 ,目的在于后面判定"b[i].y-b[i].y<d"时,只要发现一个不满足,后面的一定都不满足,循环终止
for(int i=1;i<k;i++){//暴力枚举5个点
//从该点u上面的一个点v_1开始,逐渐向上枚举点v_i ,求u->v_i之间的距离
//不需要枚举u下面的点v_j,因为这些情况在枚举v_j时就求过了v_j->u了(结合图像理解!)
for(int j=i+1;j<=k&&b[i].y-b[i].y<d;j++){//"b[i].y-b[i].y<d"即 两个点的y差值<d,如果y差值都>=d,它们间的距离不可能<d,没必要继续下去了
d=min(d,dis(b[i],b[j]));
}
}
rtn d;
}
signed main(){
cin>>n;
for(i1n)cin>>a[i].x>>a[i].y;
sort(a+1,a+n+1,cmp);
printf("%.4lf",solve(1,n));
return 0;
}
P7883 平面最近点对(加强加强版)代码
原题:P1257 平面上的最接近点对 代码
平面最近点对(加强加强版)¶
给定 \(n\) 个二维欧几里得平面上的点 \(p_1, p_2, \dots, p_n\),请输出距离最近的两个点的距离。
对于 \(100 \%\) 的数据,\(2 \leq n \leq 4 \times 10^5\),\(-10^7 \leq x_i, y_i \leq 10^7\)。
本题目标复杂度是 \(O(n \log ^2 n)\)。设置 350ms 时限的原因是:
- \(O(n \log ^2 n)\) 参考代码使用
cin不会 TLE。最快的 std 能 \(<\) 100ms。
思路¶
这题我们来用kd树解决。kd树模板——上线!