搜索优化¶
迭代加深¶
226 迭代加深 Addition Chains_哔哩哔哩_bilibili

核心代码
int dep=1;
while(!dfs(1))d++;//一直d++找到找到答案
...
例题 #1¶
Addition Chains
题目描述
一个与 \(n\) 有关的整数加成序列 \(<a_0,a_1,a_2,...,a_m>\) 满足以下四个条件: $1.a_0=1 $$2.a_m=n $$3.a_0<a_1<a_2<...<a_{m-1}<a_m $\(4.\) 对于每一个 \(k(1≤k≤m)\) 都存在有两个整数 \(i\) 和 \(j(0≤i,j≤k-1,i\) 和 \(j\) 可以相等 \()\) ,使得 $a_k=a_i+a_j $你的任务是:给定一个整数 \(n\) ,找出符合上述四个条件的长度最小的整数加成序列。如果有多个满足要求的答案,只需要输出任意一个解即可。 举个例子,序列 \(<1,2,3,5>\) 和 \(<1,2,4,5>\) 均为 \(n=5\) 时的解。
输入格式
输入包含多组数据。每组数据仅一行包含一个整数 \(n(1≤n≤10000)\) 。在最后一组数据之后是一个 \(0\) 。
输出格式
对于每组数据,输出一行所求的整数加成序列,每个整数之间以空格隔开。
感谢@Iowa_BattleShip 提供的翻译
代码
UVA不忽略行末空格!
/*
Keyblinds Guide
###################
@Ntsc 2024
- Ctrl+Alt+G then P : Enter luogu problem details
- Ctrl+Alt+B : Run all cases in CPH
- ctrl+D : choose this and dump to the next
- ctrl+Shift+L : choose all like this
- ctrl+K then ctrl+W: close all
- Alt+la/ra : move mouse to pre/nxt pos'
*/
#include <bits/stdc++.h>
#include <queue>
using namespace std;
#define rep(i, l, r) for (int i = l, END##i = r; i <= END##i; ++i)
#define per(i, r, l) for (int i = r, END##i = l; i >= END##i; --i)
#define pb push_back
#define mp make_pair
#define int long long
#define ull unsigned long long
#define pii pair<int, int>
#define ps second
#define pf first
// #define innt int
#define itn int
// #define inr intw
// #define mian main
// #define iont int
#define rd read()
int read(){
int xx = 0, ff = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
ff = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
xx = xx * 10 + (ch - '0'), ch = getchar();
return xx * ff;
}
void write(int out) {
if (out < 0)
putchar('-'), out = -out;
if (out > 9)
write(out / 10);
putchar(out % 10 + '0');
}
#define ell dbg('\n')
const char el='\n';
const bool enable_dbg = 1;
template <typename T,typename... Args>
void dbg(T s,Args... args) {
if constexpr (enable_dbg){
cerr << s;
if(1)cerr<<' ';
if constexpr (sizeof...(Args))
dbg(args...);
}
}
#define zerol = 1
#ifdef zerol
#define cdbg(x...) do { cerr << #x << " -> "; err(x); } while (0)
void err() { cerr << endl; }
template<template<typename...> class T, typename t, typename... A>
void err(T<t> a, A... x) { for (auto v: a) cerr << v << ' '; err(x...); }
template<typename T, typename... A>
void err(T a, A... x) { cerr << a << ' '; err(x...); }
#else
#define dbg(...)
#endif
const int N = 3e5 + 5;
const int INF = 1e18;
const int M = 1e7;
const int MOD = 1e9 + 7;
int n;
int dep;
itn p[N];
bool dfs(int x){
if(x>dep){
// for(int i=1;i<=dep;i++){
// cerr<<p[i]<<' ';
// }
// cerr<<endl;
if(p[x-1]==n){
for(int i=1;i<dep;i++){
write(p[i]);
putchar(' ');
}
write(p[dep]);
puts("");
// f=1;
return 1;
}
return 0;
}
int f=0;
for(int i=x-1;i;i--){
for(int j=x-1;j;j--){// 剪枝
p[x]=p[i]+p[j];
int t=p[x];
for(int k=x+1;k<=dep;k++)t<<=1;// 巨大剪枝,后一项最多是前一项的2倍
if(t<n)break;
f|=dfs(x+1);
if(f)return 1;
}
}
return f;
}
void solve(){
p[1]=1;
n=rd;
if(!n)exit(0);
dep=ceil(log2(n));
if(n==1){
cout<<1<<endl;
return ;
}
while(!dfs(2))dep++;
}
signed main() {
// freopen(".in","r",stdin);
// freopen(".in","w",stdout);
int T=1;
while(T){
solve();
}
return 0;
}
折半搜索 meet in the middle¶
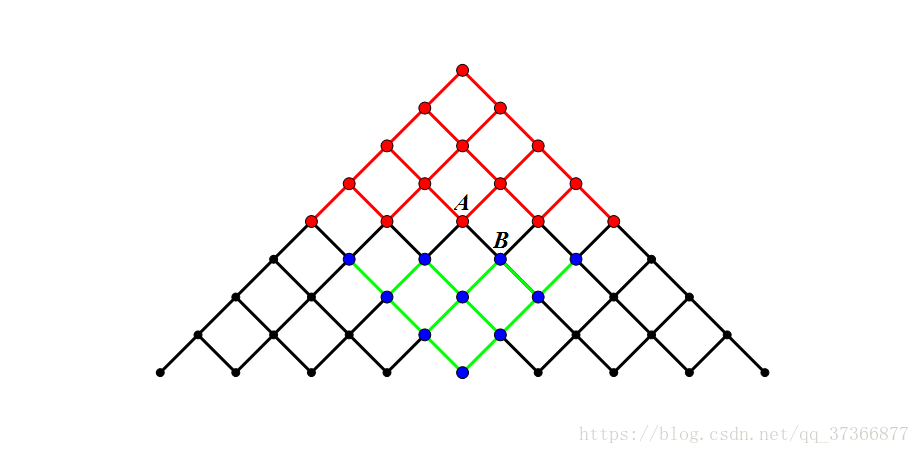
折半搜索可以让我们用\(O(2n^{\frac{k}{2}})\)完成O(n^k)的搜索。
具体实现看图
例题 #1 [CEOI2015 Day2] 世界冰球锦标赛¶
题目描述
译自 CEOI2015 Day2 T1「Ice Hockey World Championship」
今年的世界冰球锦标赛在捷克举行。Bobek 已经抵达布拉格,他不是任何团队的粉丝,也没有时间观念。他只是单纯的想去看几场比赛。如果他有足够的钱,他会去看所有的比赛。不幸的是,他的财产十分有限,他决定把所有财产都用来买门票。
给出 Bobek 的预算和每场比赛的票价,试求:如果总票价不超过预算,他有多少种观赛方案。如果存在以其中一种方案观看某场比赛而另一种方案不观看,则认为这两种方案不同。
输入格式
第一行,两个正整数 \(N\) 和 \(M(1 \leq N \leq 40,1 \leq M \leq 10^{18})\),表示比赛的个数和 Bobek 那家徒四壁的财产。
第二行,\(N\) 个以空格分隔的正整数,均不超过 \(10^{16}\),代表每场比赛门票的价格。
输出格式
输出一行,表示方案的个数。由于 \(N\) 十分大,注意:答案 \(\le 2^{40}\)。
我们发现如果这里使用普通搜索的话时间复杂度是\(O(2^n)\)的,过不去。但是如果使用折半搜索,那么就可以变成\(O(2\times 2^{n/2})\),可以过去了。
#include <bits/stdc++.h>
#include <queue>
#define rep(l, r, i) for (int i = l, END##i = r; i <= END##i; ++i)
#define per(r, l, i) for (int i = r, END##i = l; i >= END##i; --i)
using namespace std;
#define pb push_back
#define mp make_pair
#define int long long
#define pii pair<int, int>
#define ps second
#define pf first
#define X(j) i[j]
#define Y(j) (dp[j] + (i[j] + L) * (i[j] + L))
#define rd read()
int read() {
int xx = 0, ff = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
ff = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
xx = xx * 10 + (ch - '0'), ch = getchar();
return xx * ff;
}
void write(int out) {
if (out < 0)
putchar('-'), out = -out;
if (out > 9)
write(out / 10);
putchar(out % 10 + '0');
}
const int N = 3e6 + 5;
const int INF = 1e18;
int c[N],n,m;
int suma[N],sumb[N];
int cnta,cntb;
void dfs(int l,int r,int sum,int a[],int& cnt){
if(sum>m)return ;
if(l>r){
a[++cnt]=sum;
return ;
}
dfs(l+1,r,sum+c[l],a,cnt);
dfs(l+1,r,sum,a,cnt);
}
void solve(){
n=rd,m=rd;
for(int i=1;i<=n;i++){
c[i]=rd;
}
// cerr<<"OK";
int mid=n>>1;
dfs(1,mid,0,suma,cnta);
dfs(mid+1,n,0,sumb,cntb);
sort(suma+1,suma+1+cnta);
int ans=0;
for(int i=1;i<=cntb;i++){
ans+=upper_bound(suma+1,suma+1+cnta,m-sumb[i])-suma-1;
}
cout<<ans<<endl;
}
signed main() {
int T=1;
while(T--){
solve();
}
return 0;
}
例题 #2 送礼物¶
题目描述
作为惩罚,GY 被遣送去帮助某神牛给女生送礼物 (GY:貌似是个好差事)但是在 GY 看到礼物之后,他就不这么认为了。某神牛有 \(N\) 个礼物,且异常沉重,但是 GY 的力气也异常的大 (-_-b),他一次可以搬动重量和在 \(w\) 以下的任意多个物品。GY 希望一次搬掉尽量重的一些物品,请你告诉他在他的力气范围内一次性能搬动的最大重量是多少。
对于所有测试数据,\(1 \le N \le 46\), \(1 \le W,G[i] \le 2^{31}-1\)。
折半搜索模板了。
先折半,把两边的所有组成情况都搜出来,然后枚举左边,二分匹配最大的右边。
/*
Keyblinds Guide
###################
@Ntsc 2024
- Ctrl+Alt+G then P : Enter luogu problem details
- Ctrl+Alt+B : Run all cases in CPH
- ctrl+D : choose this and dump to the next
- ctrl+Shift+L : choose all like this
- ctrl+K then ctrl+W: close all
- Alt+la/ra : move mouse to pre/nxt pos'
*/
#include <bits/stdc++.h>
#include <queue>
using namespace std;
#define rep(i, l, r) for (int i = l, END##i = r; i <= END##i; ++i)
#define per(i, r, l) for (int i = r, END##i = l; i >= END##i; --i)
#define pb push_back
#define mp make_pair
#define int long long
#define ull unsigned long long
#define pii pair<int, int>
#define ps second
#define pf first
// #define innt int
#define itn int
// #define inr intw
// #define mian main
// #define iont int
#define rd read()
int read(){
int xx = 0, ff = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
ff = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
xx = xx * 10 + (ch - '0'), ch = getchar();
return xx * ff;
}
void write(int out) {
if (out < 0)
putchar('-'), out = -out;
if (out > 9)
write(out / 10);
putchar(out % 10 + '0');
}
#define ell dbg('\n')
const char el='\n';
const bool enable_dbg = 1;
template <typename T,typename... Args>
void dbg(T s,Args... args) {
if constexpr (enable_dbg){
cerr << s;
if(1)cerr<<' ';
if constexpr (sizeof...(Args))
dbg(args...);
}
}
#define zerol = 1
#ifdef zerol
#define cdbg(x...) do { cerr << #x << " -> "; err(x); } while (0)
void err() { cerr << endl; }
template<template<typename...> class T, typename t, typename... A>
void err(T<t> a, A... x) { for (auto v: a) cerr << v << ' '; err(x...); }
template<typename T, typename... A>
void err(T a, A... x) { cerr << a << ' '; err(x...); }
#else
#define dbg(...)
#endif
const int N = 1e7 + 5;
const int INF = 1e18;
const int M = 1e7;
const int MOD = 1e9 + 7;
int a[N],cnta;
int b[N],cntb;
int w[N];
int n,m;
void dfs(int x,int l,int r,int sum){
if(sum>m)return;
if(x>r){
a[++cnta]=sum;
return ;
}
dfs(x+1,l,r,sum+w[x]);
dfs(x+1,l,r,sum);
}
void dfs2(int x,int l,int r,int sum){
if(sum>m)return;
if(x>r){
b[++cntb]=sum;
return ;
}
dfs2(x+1,l,r,sum+w[x]);
dfs2(x+1,l,r,sum);
}
void solve(){
m=rd,n=rd;
for(int i=1;i<=n;i++){
w[i]=rd;
}
int mid=n>>1;
dfs(1,1,mid,0);
dfs2(mid+1,mid+1,n,0);
sort(b+1,b+cntb+1);
int ans=0;
for(int i=1;i<=cnta;i++){
auto loc=upper_bound(b+1,b+cntb+1,m-a[i]);
loc--;
if(*loc+a[i]>=m)continue;
ans=max(ans,*loc+a[i]);
}
cout<<ans<<endl;
}
signed main() {
// freopen(".in","r",stdin);
// freopen(".in","w",stdout);
int T=1;
while(T--){
solve();
}
return 0;
}
例题 #3 [USACO09NOV] Lights G¶
给出一张 \(n\) 个点 \(m\) 条边的无向图,每个点的初始状态都为 \(0\)。
你可以操作任意一个点,操作结束后该点以及所有与该点相邻的点的状态都会改变,由 \(0\) 变成 \(1\) 或由 \(1\) 变成 \(0\)。
你需要求出最少的操作次数,使得在所有操作完成之后所有 \(n\) 个点的状态都是 \(1\)。
输入格式
第一行两个整数 \(n, m\)。
之后 \(m\) 行,每行两个整数 \(a, b\),表示在点 \(a, b\) 之间有一条边。
输出格式
一行一个整数,表示最少需要的操作次数。
本题保证有解。
对于 \(100\%\) 的数据,\(1\le n\le35,1\le m\le595, 1\le a,b\le n\)。保证没有重边和自环。
本题正解是高斯消元 高斯消元,但是这里我们看见一使用 折半搜索 很愉快的水掉。
我们发现一个性质:一个灯被选择的次数≤1。所以我们只需要枚举每个灯选或者不选,然后模拟即可。
但是我们发现这样的时间复杂度是\(O(2^n)\)的,所以我们需要meet in the middle 来优化为\(O(2^{n/2})\)
- 注意,即使只有两种状态,并且后搜改的,也要还原!否则在回溯时会出锅。如:0 1 回溯 1 0 此时状态却是1 1
/*
Keyblinds Guide
###################
@Ntsc 2024
- Ctrl+Alt+getId then P : Enter luogu problem details
- Ctrl+Alt+B : Run all cases in CPH
- ctrl+D : choose this and dump to the next
- ctrl+Shift+L : choose all like this
- ctrl+K then ctrl+W: close all
- Alt+la/ra : move mouse to pre/nxt pos'
*/
#include <bits/stdc++.h>
#include <queue>
using namespace std;
#define rep(i, l, r) for (int i = l, END##i = r; i <= END##i; ++i)
#define per(i, r, l) for (int i = r, END##i = l; i >= END##i; --i)
#define pb push_back
#define int long long
#define ull unsigned long long
#define pii pair<int, int>
#define ps second
#define pf first
#define mp make_pair
// #define innt int
#define itn int
// #define inr intw
// #define mian main
// #define iont int
#define rd read()
int read() {
int xx = 0, ff = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
ff = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
xx = xx * 10 + (ch - '0'), ch = getchar();
return xx * ff;
}
void write(int out) {
if (out < 0)
putchar('-'), out = -out;
if (out > 9)
write(out / 10);
putchar(out % 10 + '0');
}
#define ell dbg('\n')
const char el='\n';
const bool enable_dbg = 1;
template <typename T,typename... Args>
void dbg(T s,Args... args) {
if constexpr (enable_dbg) {
cerr << s;
if(1)cerr<<' ';
if constexpr (sizeof...(Args))
dbg(args...);
}
}
#define zerol = 1
#ifdef zerol
#define cdbg(x...) do { cerr << #x << " -> "; err(x); } while (0)
void err() {
cerr << endl;
}
template<template<typename...> class T, typename t, typename... A>
void err(T<t> a, A... x) {
for (auto v: a) cerr << v << ' ';
err(x...);
}
template<typename T, typename... A>
void err(T a, A... x) {
cerr << a << ' ';
err(x...);
}
#else
#define dbg(...)
#endif
const int N = 50 + 10;
const int INF = 2e9;
const int M = 1e3 + 10;
const int MOD = 1e9 + 7;
/*
我们考虑如何匹配
因为开关一个灯会影响其他灯,所以我们枚举每个灯是否开关,状态中记录的不是
每个灯是否开关,而是最后的结果
匹配时找异或和为全集的即可。
*/
int n,m;
vector<int> e[N];
void add(int a,int b){
e[a].pb(b);
e[b].pb(a);
}
map<int,int> vis;
bitset<N> p;
int ans=INF;
void dfs(int x,int r,int cnt){
if(x>r){
int res=0;
for(int i=1;i<=n;i++){
res<<=1;
res|=p[i];
}
// cdbg(res);
if(vis[res]==0)vis[res]=cnt;
vis[res]=min(vis[res],cnt);
return ;
}
dfs(x+1,r,cnt);
for(auto v:e[x]){
p[v]=p[v]^1;
}
p[x]=p[x]^1;
dfs(x+1,r,cnt+1);
for(auto v:e[x]){
p[v]=p[v]^1;
}
p[x]=p[x]^1;
}
void dfs2(int x,int r,int cnt){
if(x>r){
int res=0;
for(int i=1;i<=n;i++){
res<<=1;
res|=p[i];
}
res=((1ll<<n)-1ll)^res;
if(vis[res])ans=min(ans,vis[res]+cnt);
if(res==0)ans=min(ans,cnt);
return ;
}
dfs2(x+1,r,cnt);
for(auto v:e[x]){
p[v]=p[v]^1;
}
p[x]=p[x]^1;
dfs2(x+1,r,cnt+1);
for(auto v:e[x]){
p[v]=p[v]^1;
}
p[x]=p[x]^1;
}
void solve(){
n=rd,m=rd;
for(int i=1;i<=m;i++){
add(rd,rd);
}
int mid=n>>1;
dfs(1,mid,0);
p.reset();
dfs2(mid+1,n,0);
cout<<ans<<endl;
}
signed main() {
// freopen("kujou.in","r",stdin);
// freopen("kujou.out","w",stdout);
int T=1;
while(T--){
solve();
}
return 0;
}