树剖题单¶
HDU5029 Relief grain¶

考虑如果只是要求一种颜色,每个节点的个数,那么我们可以用树上差分。那么这里要求多个节点,如果只是维护节点数据,我们还是可以用树上差分(对数组差分)。但是因为要维护最大值,所以要用线段树来维护。但是我们要合并多个子树的信息,因此不能用dfs过程中维护线段树,怎么办呢?用树剖将一条链分成多个串即可。
// Problem: F. Relief grain
// Contest: LibreOJ - CSP2024专题复习2
// URL: http://www.nfls.com.cn:20035/contest/2079/problem/6
// Memory Limit: 97 MB
// Time Limit: 10000 ms
// Challenger: Erica N
// ----
#include<bits/stdc++.h>
using namespace std;
#define rd read()
#define ull unsigned long long
// #define int long long
#define itn int
#define ps second
#define pf first
namespace fastOI{
#define rd read()
int read(){
int xx = 0, ff = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
ff = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
xx = xx * 10 + (ch - '0'), ch = getchar();
return xx * ff;
}
void write(int out) {
if (out < 0)
putchar('-'), out = -out;
if (out > 9)
write(out / 10);
putchar(out % 10 + '0');
}
}using namespace fastOI;
#define zerol = 1
#ifdef zerol
#define cdbg(x...) do { cerr << #x << " -> "; err(x); } while (0)
void err() {
cerr << endl;
}
template<template<typename...> class T, typename t, typename... A>
void err(T<t> a, A... x) {
for (auto v: a) cerr << v << ' ';
err(x...);
}
template<typename T, typename... A>
void err(T a, A... x) {
cerr << a << ' ';
err(x...);
}
#else
#define dbg(...)
#endif
const int N=3e5+5;
const ull P=137;
const int INF=1e9+7;
/*
策略
*/
vector<int> e[N];
void add(int a,int b){
e[a].push_back(b);
e[b].push_back(a);
}
#define pii pair<int,int>
int dep[N], sz[N],fa[N][22];
int son[N];
int top[N];
int dfn[N],_dfn[N],tim;
int ans[N];
vector<pii> cg[N];
void dfs(int x,int f){
dep[x]=dep[f]+1;
sz[x]=1;
son[x]=0;
for(auto v:e[x]){
if(v==f)continue;
fa[v][0]=x;
for(int i=1;i<=20;i++){
fa[v][i]=fa[fa[v][i-1]][i-1];
}
dfs(v,x);
sz[x]+=sz[v];
if(sz[son[x]]<sz[v])son[x]=v;
}
}
int lca(int a,int b){
if(dep[a]<dep[b])swap(a,b);
for(int i=20;~i;i--){
if(dep[fa[a][i]]>=dep[b])a=fa[a][i];
}
if(a==b)return a;
for(int i=20;~i;i--){
if(fa[a][i]!=fa[b][i])
{
a=fa[a][i];
b=fa[b][i];
}
}
return fa[a][0];
}
void dfs(int x,int fa,int tp){
top[x]=tp;
dfn[x]=++tim;
_dfn[tim]=x;
if(son[x])dfs(son[x],x,tp);
for(auto v:e[x]){
if(v==fa||v==son[x])continue;
dfs(v,x,v);
}
}
void solve(int a,int b,int c){
int anc=lca(a,b);
// cdbg(a,b,anc);
while(1){
if(dep[top[a]]<=dep[anc]){
cg[dfn[anc]].push_back({c,1});
cg[dfn[a]+1].push_back({c,-1});
break;
}
cg[dfn[top[a]]].push_back({c,1});
cg[dfn[a]+1].push_back({c,-1});
a=fa[top[a]][0];
}
while(1){
if(dep[top[b]]<=dep[anc]){
cg[dfn[anc]+1].push_back({c,1});
cg[dfn[b]+1].push_back({c,-1});
break;
}
cg[dfn[top[b]]].push_back({c,1});
cg[dfn[b]+1].push_back({c,-1});
b=fa[top[b]][0];
}
}
namespace SGT{
pii t[N<<2];
pii merge(pii a,pii b){
// cdbg(a.ps,b.ps);
if(a.pf==b.pf)return a;
return a.pf>b.pf?a:b;
}
void pushup(int x){
t[x]=merge(t[x<<1],t[x<<1|1]);
}
void change(int x,int l,int r,int p,int v){
if(l==r){
// cdbg(l);
t[x].pf+=v;
return ;
}
int mid=l+r>>1;
if(p<=mid)change(x<<1,l,mid,p,v);
else change(x<<1|1,mid+1,r,p,v);
pushup(x);
}
int query(){
if(t[1].pf==0)return 0;
// cdbg(t[1].pf);
return t[1].ps;
}
void build(int x,int l,int r){
if(l==r){
t[x]={0,l};
return ;
}
int mid=l+r>>1;
build(x<<1,l,mid);
build(x<<1|1,mid+1,r);
pushup(x);
}
}using namespace SGT;
void solve(){
// memset(fa,0,sizeof fa);
// memset(top,0,sizeof top);
// memset(dep,0,sizeof dep);
// memset(sz,0,sizeof sz);
// memset(dfn,0,sizeof dfn);
// memset(_dfn,0,sizeof _dfn);
// memset(ans,0,sizeof ans);
int n=rd,m=rd;
tim=0;
if(!n)exit(0);
for(int i=1;i<n;i++){
add(rd,rd);
}
build(1,1,100000);
dfs(1,0);
dfs(1,0,1);
// cdbg(top[2]);
while(m--){
int a=rd,b=rd,c=rd;
solve(a,b,c);
}
for(itn i=1;i<=n;i++){
while(cg[i].size()){
auto v=cg[i].back();
// cdbg(i,v.pf,v.ps);
change(1,1,100000,v.pf,v.ps);
cg[i].pop_back();
}
// cdbg(_dfn[i],query());
ans[_dfn[i]]=query();
}
while(cg[n+1].size())cg[n+1].pop_back();
for(int i=1;i<=n;i++){
cout<<ans[i]<<endl;
}
for(int i=1;i<=n;i++){
while(e[i].size()){
e[i].pop_back();
}
}
}
signed main(){
while(1){
solve();
}
}
Play with tree¶
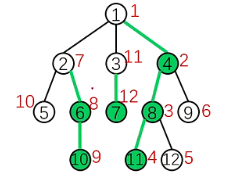
发现操作实际上是:
-
将路径上边权变为c
-
设路径上边权最小值为mn,将路径上边权减去min(-c,mn)
那么就是树剖板子。
// Problem: G. Play with tree
// Contest: LibreOJ - CSP2024专题复习2
// URL: http://www.nfls.com.cn:20035/contest/2079/problem/7%E3%80%81
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// Challenger: Erica N
// ----
#pragma GCC optimize("O2")
#pragma GCC optimize("O3")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#include<bits/stdc++.h>
using namespace std;
#define rd read()
#define ull unsigned long long
// #define int long long
#define itn int
#define ps second
#define pf first
namespace fastOI{
#define rd read()
int read(){
int xx = 0, ff = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
ff = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
xx = xx * 10 + (ch - '0'), ch = getchar();
return xx * ff;
}
void write(int out) {
if (out < 0)
putchar('-'), out = -out;
if (out > 9)
write(out / 10);
putchar(out % 10 + '0');
}
}using namespace fastOI;
#define zerol = 1
#ifdef zerol
#define cdbg(x...) do { cerr << #x << " -> "; err(x); } while (0)
void err() {
cerr << endl;
}
template<template<typename...> class T, typename t, typename... A>
void err(T<t> a, A... x) {
for (auto v: a) cerr << v << ' ';
err(x...);
}
template<typename T, typename... A>
void err(T a, A... x) {
cerr << a << ' ';
err(x...);
}
#else
#define dbg(...)
#endif
const int N=3e5+5;
const ull P=137;
const int INF=1e9+7;
/*
策略
*/
vector<int> e[N];
void add(int a,int b){
e[a].push_back(b);
e[b].push_back(a);
}
#define pii pair<int,int>
int n,m;
int dep[N], sz[N],fa[N];
int son[N];
int top[N];
int dfn[N],_dfn[N],tim;
int ans[N];
vector<pii> cg[N];
void dfs(int x,int f){
dep[x]=dep[f]+1;
sz[x]=1;
son[x]=0;
for(auto v:e[x]){
if(v==f)continue;
fa[v]=x;
dfs(v,x);
sz[x]+=sz[v];
if(sz[son[x]]<sz[v])son[x]=v;
}
}
// int lca(int a,int b){
// if(dep[a]<dep[b])swap(a,b);
// for(int i=20;~i;i--){
// if(dep[fa[a][i]]>=dep[b])a=fa[a][i];
// }
// if(a==b)return a;
// for(int i=20;~i;i--){
// if(fa[a][i]!=fa[b][i])
// {
// a=fa[a][i];
// b=fa[b][i];
// }
// }
// return fa[a][0];
// }
void dfs(int x,int fa,int tp){
top[x]=tp;
dfn[x]=++tim;
_dfn[tim]=x;
if(son[x])dfs(son[x],x,tp);
for(auto v:e[x]){
if(v==fa||v==son[x])continue;
dfs(v,x,v);
}
}
namespace SGT{
pii t[N<<2]; // val,cnt
int tagAdd[N<<2],tagFill[N<<2];
//fill覆盖add
pii merge(pii a,pii b){
pii r;
if(a.pf==b.pf){r={a.pf,a.ps+b.ps};return r;}
return a.pf<b.pf?a:b;
}
void pushup(int x){
t[x]=merge(t[x<<1],t[x<<1|1]);
}
void addtagFill(int x,int v){
tagFill[x]=v;
tagAdd[x]=0;
t[x]={v,1};
}
void addtagAdd(int x,int v){
t[x].pf+=v;
if(~tagFill[x])tagFill[x]+=v;
else tagAdd[x]+=v;
}
void pushdown(int x){
if(~tagFill[x]){
addtagFill(x<<1,tagFill[x]);
addtagFill(x<<1|1,tagFill[x]);
tagFill[x]=-1;
}
if(tagAdd[x]){
addtagFill(x<<1,tagAdd[x]);
addtagFill(x<<1|1,tagAdd[x]);
tagAdd[x]=0;
}
}
void changeFill(int x,int l,int r,int pl,int pr,int v){
if(pr<pl)return ;
if(l==r){
// cdbg(l);
addtagFill(x,v);
return ;
}
pushdown(x);
int mid=l+r>>1;
if(pl<=mid)changeFill(x<<1,l,mid,pl,pr,v);
if(pr>mid)changeFill(x<<1|1,mid+1,r,pl,pr,v);
pushup(x);
}
void changeAdd(int x,int l,int r,int pl,int pr,int v){
if(pr<pl)return ;
if(l==r){
addtagAdd(x,v);
return ;
}
pushdown(x);
int mid=l+r>>1;
if(pl<=mid)changeAdd(x<<1,l,mid,pl,pr,v);
if(pr>mid)changeAdd(x<<1|1,mid+1,r,pl,pr,v);
pushup(x);
}
pii queryMin(int x,int l,int r,int pl,int pr){
// if(pl==1)pl=2;
if(pr<pl)return make_pair(INF,0); //!!!
if(pl<=l&&pr>=r)return t[x];
pushdown(x);
int mid=l+r>>1;
int fl=0,fr=0;
pii nl,nr;
if(pl<=mid)fl=1,nl=queryMin(x<<1,l,mid,pl,pr);
if(pr>mid)fr=1,nr=queryMin(x<<1|1,mid+1,r,pl,pr);
if(fl+fr==1){
if(fl)return nl;
else return nr;
}
return merge(nl,nr);
}
void build(int x,int l,int r){
tagFill[x]=-1;
if(l==r){
t[x]={0,1};
return ;
}
int mid=l+r>>1;
build(x<<1,l,mid);
build(x<<1|1,mid+1,r);
pushup(x);
}
}using namespace SGT;
int queryRoadMin(int u,int v){
int res=INF;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]])swap(u,v);//交换,使得u所在的重链top恒比v的深 ,即保证是更深的在往上跳而不是浅的一直在往上跳
res=min(res,queryMin(1,1,n,dfn[top[u]],dfn[u]).pf);//注意id[top[u]]<=id[u]
u=fa[top[u]];
}
if(dep[u]>dep[v])swap(u,v);
res=min(res,queryMin(1,1,n,dfn[u]+1,dfn[v]).pf);
return res;
}
void changeRoadAdd(int u,int v,int c){
int res=0;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]])swap(u,v);//交换,使得u所在的重链top恒比v的深 ,即保证是更深的在往上跳而不是浅的一直在往上跳
changeAdd(1,1,n,dfn[top[u]],dfn[u],c);//注意id[top[u]]<=id[u]
u=fa[top[u]];
}
if(dep[u]>dep[v])swap(u,v);
changeAdd(1,1,n,dfn[u]+1,dfn[v],c);
}
void changeRoadFill(int u,int v,int c){
int res=0;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]])swap(u,v);//交换,使得u所在的重链top恒比v的深 ,即保证是更深的在往上跳而不是浅的一直在往上跳
changeFill(1,1,n,dfn[top[u]],dfn[u],c);//注意id[top[u]]<=id[u]
u=fa[top[u]];
}
if(dep[u]>dep[v])swap(u,v);
changeFill(1,1,n,dfn[u]+1,dfn[v],c);
}
signed main(){
n=rd,m=rd;
for(int i=1;i<n;i++){
add(rd,rd);
}
dfs(1,0);
dfs(1,0,1);
build(1,1,n);
changeFill(1,1,n,1,1,INF);
while(m--){
int op=rd,a=rd,b=rd,c=rd;
if(op==1){
changeRoadFill(a,b,c);
}else{
itn mn=queryRoadMin(a,b);
// c=-c;
// cdbg(mn);
changeRoadAdd(a,b,max(-mn,c));
}
// for(int i=1;i<=n;i++)cdbg(queryMin(1,1,n,dfn[i],dfn[i]).pf);
// cdbg("");
auto v=queryMin(1,1,n,2,n);
int res=v.ps;
if(v.pf!=0)res=0;
write(res);
puts("");
}
}
// Problem: G. Play with tree
// Contest: LibreOJ - CSP2024专题复习2
// URL: http://www.nfls.com.cn:20035/contest/2079/problem/7%E3%80%81
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// Challenger: Erica N
// ----
#pragma GCC optimize("O2")
#pragma GCC optimize("O3")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#include<bits/stdc++.h>
using namespace std;
#define rd read()
#define ull unsigned long long
// #define int long long
#define itn int
#define ps second
#define pf first
namespace fastOI{
#define rd read()
int read(){
int xx = 0, ff = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
ff = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
xx = xx * 10 + (ch - '0'), ch = getchar();
return xx * ff;
}
void write(int out) {
if (out < 0)
putchar('-'), out = -out;
if (out > 9)
write(out / 10);
putchar(out % 10 + '0');
}
}using namespace fastOI;
#define zerol = 1
#ifdef zerol
#define cdbg(x...) do { cerr << #x << " -> "; err(x); } while (0)
void err() {
cerr << endl;
}
template<template<typename...> class T, typename t, typename... A>
void err(T<t> a, A... x) {
for (auto v: a) cerr << v << ' ';
err(x...);
}
template<typename T, typename... A>
void err(T a, A... x) {
cerr << a << ' ';
err(x...);
}
#else
#define dbg(...)
#endif
const int N=3e5+5;
const ull P=137;
const int INF=1e9+7;
/*
策略
*/
vector<int> e[N];
void add(int a,int b){
e[a].push_back(b);
e[b].push_back(a);
}
#define pii pair<int,int>
int n,m;
int dep[N], sz[N],fa[N][22];
int son[N];
int top[N];
int dfn[N],_dfn[N],tim;
int ans[N];
vector<pii> cg[N];
void dfs(int x,int f){
dep[x]=dep[f]+1;
sz[x]=1;
son[x]=0;
for(auto v:e[x]){
if(v==f)continue;
fa[v][0]=x;
for(int i=1;i<=20;i++){
fa[v][i]=fa[fa[v][i-1]][i-1];
}
dfs(v,x);
sz[x]+=sz[v];
if(sz[son[x]]<sz[v])son[x]=v;
}
}
int lca(int a,int b){
if(dep[a]<dep[b])swap(a,b);
for(int i=20;~i;i--){
if(dep[fa[a][i]]>=dep[b])a=fa[a][i];
}
if(a==b)return a;
for(int i=20;~i;i--){
if(fa[a][i]!=fa[b][i])
{
a=fa[a][i];
b=fa[b][i];
}
}
return fa[a][0];
}
void dfs(int x,int fa,int tp){
top[x]=tp;
dfn[x]=++tim;
_dfn[tim]=x;
if(son[x])dfs(son[x],x,tp);
for(auto v:e[x]){
if(v==fa||v==son[x])continue;
dfs(v,x,v);
}
}
namespace SGT{
pii t[N<<2]; // val,cnt
int tagAdd[N<<2],tagFill[N<<2];
//fill覆盖add
pii merge(pii a,pii b){
pii r;
if(a.pf==b.pf){r={a.pf,a.ps+b.ps};return r;}
return a.pf<b.pf?a:b;
}
void pushup(int x){
t[x]=merge(t[x<<1],t[x<<1|1]);
}
void addtagFill(int x,int v){
tagFill[x]=v;
tagAdd[x]=0;
t[x]={v,1};
}
void addtagAdd(int x,int v){
t[x].pf+=v;
if(~tagFill[x])tagFill[x]+=v;
else tagAdd[x]+=v;
}
void pushdown(int x){
if(~tagFill[x]){
addtagFill(x<<1,tagFill[x]);
addtagFill(x<<1|1,tagFill[x]);
tagFill[x]=-1;
}
if(tagAdd[x]){
addtagFill(x<<1,tagAdd[x]);
addtagFill(x<<1|1,tagAdd[x]);
tagAdd[x]=0;
}
}
void changeFill(int x,int l,int r,int pl,int pr,int v){
if(pr<pl)return ;
if(l==r){
// cdbg(l);
addtagFill(x,v);
return ;
}
pushdown(x);
int mid=l+r>>1;
if(pl<=mid)changeFill(x<<1,l,mid,pl,pr,v);
if(pr>mid)changeFill(x<<1|1,mid+1,r,pl,pr,v);
pushup(x);
}
void changeAdd(int x,int l,int r,int pl,int pr,int v){
if(pr<pl)return ;
if(l==r){
addtagAdd(x,v);
return ;
}
pushdown(x);
int mid=l+r>>1;
if(pl<=mid)changeAdd(x<<1,l,mid,pl,pr,v);
if(pr>mid)changeAdd(x<<1|1,mid+1,r,pl,pr,v);
pushup(x);
}
pii queryMin(int x,int l,int r,int pl,int pr){
// if(pl==1)pl=2;
if(pr<pl)return make_pair(INF,0); //!!!
if(pl<=l&&pr>=r)return t[x];
pushdown(x);
int mid=l+r>>1;
int fl=0,fr=0;
pii nl,nr;
if(pl<=mid)fl=1,nl=queryMin(x<<1,l,mid,pl,pr);
if(pr>mid)fr=1,nr=queryMin(x<<1|1,mid+1,r,pl,pr);
if(fl+fr==1){
if(fl)return nl;
else return nr;
}
return merge(nl,nr);
}
void build(int x,int l,int r){
tagFill[x]=-1;
if(l==r){
t[x]={0,1};
return ;
}
int mid=l+r>>1;
build(x<<1,l,mid);
build(x<<1|1,mid+1,r);
pushup(x);
}
}using namespace SGT;
int queryRoadMin(int a,int b){
int res=INF;
int anc=lca(a,b);
// cdbg(a,b,anc);
while(1){
if(dep[top[a]]<=dep[anc]){
res=min(res,queryMin(1,1,n,dfn[anc]+1,dfn[a]).pf);
// cdbg(anc,a,res);
break;
}
res=min(res,queryMin(1,1,n,dfn[top[a]],dfn[a]).pf);
// cdbg(top[a],a,res);
a=fa[top[a]][0];
}
while(1){
if(dep[top[b]]<=dep[anc]){
res=min(res,queryMin(1,1,n,dfn[anc]+1,dfn[b]).pf);
// cdbg(anc,b,res);
break;
}
res=min(res,queryMin(1,1,n,dfn[top[b]],dfn[b]).pf);
// cdbg(top[b],b);
b=fa[top[b]][0];
}
// cdbg(res);
return res;
}
void changeRoadAdd(int a,int b,int c){
int anc=lca(a,b);
// cdbg(a,b,anc);
while(1){
if(dep[top[a]]<=dep[anc]){
changeAdd(1,1,n,dfn[anc]+1,dfn[a],c);
break;
}
changeAdd(1,1,n,dfn[top[a]],dfn[a],c);
a=fa[top[a]][0];
}
while(1){
if(dep[top[b]]<=dep[anc]){
changeAdd(1,1,n,dfn[anc]+1,dfn[b],c);
break;
}
changeAdd(1,1,n,dfn[top[b]],dfn[b],c);
b=fa[top[b]][0];
}
}
void changeRoadFill(int a,int b,int c){
int anc=lca(a,b);
// cdbg(a,b,anc);
while(1){
if(dep[top[a]]<=dep[anc]){
changeFill(1,1,n,dfn[anc]+1,dfn[a],c);
break;
}
changeFill(1,1,n,dfn[top[a]],dfn[a],c);
a=fa[top[a]][0];
}
while(1){
if(dep[top[b]]<=dep[anc]){
changeFill(1,1,n,dfn[anc]+1,dfn[b],c);
break;
}
changeFill(1,1,n,dfn[top[b]],dfn[b],c);
b=fa[top[b]][0];
}
}
signed main(){
n=rd,m=rd;
for(int i=1;i<n;i++){
add(rd,rd);
}
dfs(1,0);
dfs(1,0,1);
build(1,1,n);
while(m--){
int op=rd,a=rd,b=rd,c=rd;
if(op==1){
changeRoadFill(a,b,c);
}else{
itn mn=queryRoadMin(a,b);
// c=-c;
// cdbg(mn);
changeRoadAdd(a,b,max(-mn,c));
}
// for(int i=1;i<=n;i++)cdbg(queryMin(1,1,n,dfn[i],dfn[i]).pf);
// cdbg("");
auto v=queryMin(1,1,n,2,n);
int res=v.ps;
if(v.pf!=0)res=0;
write(res);
puts("");
}
}
[SDOI2011] 染色¶
题目描述
给定一棵 \(n\) 个节点的无根树,共有 \(m\) 个操作,操作分为两种:
-
将节点 \(a\) 到节点 \(b\) 的路径上的所有点(包括 \(a\) 和 \(b\))都染成颜色 \(c\)。
-
询问节点 \(a\) 到节点 \(b\) 的路径上的颜色段数量。
颜色段的定义是极长的连续相同颜色被认为是一段。例如 112221 由三段组成:11、222、1。
输入格式
输入的第一行是用空格隔开的两个整数,分别代表树的节点个数 \(n\) 和操作个数 \(m\)。
第二行有 \(n\) 个用空格隔开的整数,第 \(i\) 个整数 \(w_i\) 代表结点 \(i\) 的初始颜色。
第 \(3\) 到第 \((n + 1)\) 行,每行两个用空格隔开的整数 \(u, v\),代表树上存在一条连结节点 \(u\) 和节点 \(v\) 的边。
第 \((n + 2)\) 到第 \((n + m + 1)\) 行,每行描述一个操作,其格式为:
每行首先有一个字符 \(op\),代表本次操作的类型。
-
若 \(op\) 为
C,则代表本次操作是一次染色操作,在一个空格后有三个用空格隔开的整数 \(a, b, c\),代表将 \(a\) 到 \(b\) 的路径上所有点都染成颜色 \(c\)。 -
若 \(op\) 为
Q,则代表本次操作是一次查询操作,在一个空格后有两个用空格隔开的整数 \(a, b\),表示查询 \(a\) 到 \(b\) 路径上的颜色段数量。
输出格式
对于每次查询操作,输出一行一个整数代表答案。
数据规模与约定
对于 \(100\%\) 的数据,\(1 \leq n, m \leq 10^5\),\(1 \leq w_i, c \leq 10^9\),\(1 \leq a, b, u, v \leq n\),\(op\) 一定为 C 或 Q,保证给出的图是一棵树。
除原数据外,还存在一组不计分的 hack 数据。
非倍增LCA的树剖写法:
每次从top更深的点往上跳,直到top相同。
此时两点在同一个链上,判断那个深浅即可。
// Problem: P2486 [SDOI2011] 染色
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2486
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Challenger: Erica N
// ----
#include<bits/stdc++.h>
using namespace std;
#define rd read()
#define ull unsigned long long
#define int long long
#define itn int
#define ps second
#define pf first
int read(){
int x;
cin>>x;
return x;
}
#define zerol = 1
#ifdef zerol
#define cdbg(x...) do { cerr << #x << " -> "; err(x); } while (0)
void err() {
cerr << endl;
}
template<template<typename...> class T, typename t, typename... A>
void err(T<t> a, A... x) {
for (auto v: a) cerr << v << ' ';
err(x...);
}
template<typename T, typename... A>
void err(T a, A... x) {
cerr << a << ' ';
err(x...);
}
#else
#define dbg(...)
#endif
const int N=3e5+5;
const ull P=137;
const int INF=1e9+7;
/*
策略
*/
int sz[N],dep[N],son[N],dfn[N],tim,top[N],a[N];
int fa[N];
int _dfn[N];
int n,m;
vector<int> e[N];
void add(itn a,int b){
e[a].push_back(b);
e[b].push_back(a);
}
void dfs(int x,int f){
dep[x]=dep[f]+1;
sz[x]=1;
for(auto v:e[x]){
if(v==f)continue;
fa[v]=x;
dfs(v,x);
sz[x]+=sz[v];
if(sz[son[x]]<sz[v])son[x]=v;
}
}
void dfs(int x,int f,int tp){
dfn[x]=++tim;
_dfn[tim]=x;
top[x]=tp;
if(son[x])dfs(son[x],x,tp);
for(auto v:e[x]){
if(v==f||v==son[x])continue;
dfs(v,x,v);
}
}
namespace SGT{
struct Node{
itn lc,rc,cnt;
}t[N<<2];
int tag[N<<2];
Node merge(Node a,Node b){
// cdbg(a.cnt,b.cnt);
if(a.lc+a.rc==0)return b;
if(b.lc+b.rc==0)return a;
Node r={a.lc,b.rc,a.cnt+b.cnt};
if(a.rc==b.lc)r.cnt--;
return r;
}
void pushup(int x){
t[x]=merge(t[x<<1],t[x<<1|1]);
}
void addtag(int x,itn c){
t[x]={c,c,1};
tag[x]=c;
}
void pushdown(int x){
if(tag[x]){
addtag(x<<1,tag[x]);
addtag(x<<1|1,tag[x]);
tag[x]=0;
}
}
void change(int x,int l,int r,int pl,int pr,int v){
if(pl<=l&&pr>=r){
addtag(x,v);
return ;
}
pushdown(x);
int mid=l+r>>1;
if(pl<=mid)change(x<<1,l,mid,pl,pr,v);
if(pr>mid)change(x<<1|1,mid+1,r,pl,pr,v);
pushup(x);
}
Node query(itn x,int l,int r,int pl,itn pr){
if(pl<=l&&pr>=r){
return t[x];
}
pushdown(x);
int fl=0,fr=0;
Node nl,nr;
int mid=l+r>>1;
if(pl<=mid)fl=1,nl=query(x<<1,l,mid,pl,pr);
if(pr>mid)fr=1,nr=query(x<<1|1,mid+1,r,pl,pr);
if(fl+fr==1){
if(fl)return nl;
return nr;
}
return merge(nl,nr);
}
void build(itn x,int l,int r){
if(l==r){
t[x]={a[_dfn[l]],a[_dfn[l]],1}; //!!!
return ;
}
int mid=l+r>>1;
build(x<<1,l,mid);
build(x<<1|1,mid+1,r);
pushup(x);
}
}using namespace SGT;
void changeRoad(int a,itn b,int c){
while(top[a]!=top[b]){
if(dep[top[a]]<dep[top[b]])swap(a,b);
change(1,1,n,dfn[top[a]],dfn[a],c);
a=fa[top[a]];
}
if(dep[a]<dep[b])swap(a,b);
change(1,1,n,dfn[b],dfn[a],c);
}
int queryRoad(int a,itn b){
Node l={0,0,0},r={0,0,0};
int op=1;
while(top[a]!=top[b]){
if(dep[top[a]]<dep[top[b]])swap(a,b),op^=1;
Node cur=query(1,1,n,dfn[top[a]],dfn[a]);
// cdbg(top[a],a,cur.cnt,op,cur.lc,cur.rc);
if(op)r=merge(cur,r);
else swap(cur.lc,cur.rc),l=merge(l,cur);
a=fa[top[a]];
}
if(dep[a]<dep[b])swap(a,b),op^=1;
Node cur=query(1,1,n,dfn[b],dfn[a]);
// cdbg(b,a,cur.cnt,op);
// cdbg(l.lc,l.rc,r.lc,r.rc,cur.lc,cur.rc);
if(op){
r=merge(cur,r);
// swap(l.lc,l.rc);
l=merge(l,r);
}else{
swap(cur.lc,cur.rc),l=merge(l,cur);
// swap(l.lc,l.rc);
l=merge(l,r);
}
return l.cnt;
}
signed main(){
n=rd,m=rd;
for(int i=1;i<=n;i++){
a[i]=rd;
}
for(int i=1;i<n;i++){
add(rd,rd);
}
dfs(1,0);
dfs(1,0,1);
build(1,1,n);
while(m--){
// cdbg(m);
char op;
cin>>op;
if(op=='C'){
itn a=rd,b=rd,c=rd;
changeRoad(a,b,c);
}else{
int a=rd,b=rd;
cout<<queryRoad(a,b)<<endl;
}
}
}