李超线段树¶

要求在平面直角坐标系下维护两个操作：

在平面上加入一条线段。记第 \(i\) 条被插入的线段的标号为 \(i\)。
给定一个数 \(k\)，询问与直线 \(x = k\) 相交的线段中，交点纵坐标最大的线段的编号。

本题输入强制在线。

思路¶

先看看题目，我们要维护的是什么？是对于每个 \(x\)，其上方最高的线段是那一条。我们想到，当我们往图中加入一条新的线段时，假如这条线段在某个区间是最高的，那么我们就需要把这个区间的答案都修改为这个线段。所以很明显我们可以考虑用类似线段树的数据结构来维护。

但是首先要明确一点，每次加入一条线段可能要修改多个区间，也有可能一个区间都不修改。

我们从线段树的模板上来修改。

修改¶

首先是修改函数。这里我们要实现的功能是添加一条线段，然后修改对应的值。

void change(int x,int l,int r,int ql,int qr,int v){
    if(l>=ql&&r<=qr){
        pushup(x,l,r,v);return ;
    }
    int mid=(l+r)>>1;
    if(ql<=mid)change(x<<1,l,mid,ql,qr,v);
    if(qr>mid)change(x<<1|1,mid+1,r,ql,qr,v);
}

这里的代码还是比较简洁的。注意这里应该是拿区间修改的线段树模板来修改（注意最后两行）而不是单点修改的。

解释一下这里的 \(v\)，这里的 \(v\) 是插入的线段是编号。我们开一个结构体 line{k,b} 来记录每一条线段的 \(k,b\)，然后我们使用数组 lne[] 来记录所有线段。

当我们访问到一个区间在要修改的区间 \([ ql,qr]\) 之内时，我们就需要修改这个区间内的信息了。我们使用 pushup() 函数来修改（实际上叫做 update 更好，但由于是线段树改的，我们姑且叫他 pushup）。

void pushup(int x,int l,int r,int u){//ok
    int &v=s[x];
    int mid=(l+r)>>1,bmid=cmp(cal(u,mid),cal(v,mid));
    if(bmid==1||(!bmid&&u<v))swap(u,v);

    int bl=cmp(cal(u,l),cal(v,l));
    int br=cmp(cal(u,r),cal(v,r));

    if(bl==1||(!bl&&u<v))pushup(x<<1,l,mid,u);
    if(br==1||(!br&&u<v))pushup(x<<1|1,mid+1,r,u);  
}

这里的 s[] 数组就相当于线段树中的每个节点，在我的线段树板子里就是 tr[] 数组。我们这颗线段树记录的是“区间最高的线段的编号”，所以 \(s\) 中记录的信息是线段的编号。那么这里的 \(x\) 就是线段树上的节点的编号，s[x] 就是原来这个节点上记录的线段的编号。我们要比较这个就线段 \(v\) 和我们新加入的线段 \(u\) 的高度关系，并且考虑更新 s[x]。

这里我们需要两个辅助函数。

int cmp(double x, double y) {
  if (x-y>eps) return 1;
  if (y-x>eps) return -1;
  return 0;
}

db cal(int id,int p){//
    return 1.00*lne[id].b+p*lne[id].k;//计算直线id在x=p处的y
}

第一个是比较大小的。这个不用说了，因为小数运算会出现精度问题。

第二个我来解释一下，其实也没什么，就是我们传入线段的编号和当前的 \(x\)，计算这条线段在 \(x=p\) 时的 \(y\) 值（即高度值）。

我们再回到 pushup 函数。

第一步，我们先计算当 \(x=mid\) 时两个线段的高度关系。假设线段 \(u\)（记住在该例子里 \(u\) 是新加入的线段）在 \(x =mid\) 时的高度大于 \(v\) 的，那么我们就把 \(u,v\) 交换一下，有利于减少讨论情况。注意这里不仅仅是简单交换值，而是把映射关系也交换了。

在交换之后，我们就默认 \(u\) 在 \(x=mid\) 处比 \(v\) 低了。那么这时我们来分类讨论一下。我们记录 \(4\) 个端点的高度值 \(ul,ur,vl,vr\)。

当 \(vl≥ul\) 且 \(vr≥ur\) 时，在 \([l,r]\) 中 \(u\) 肯定不如 \(v\)。相反也如此。
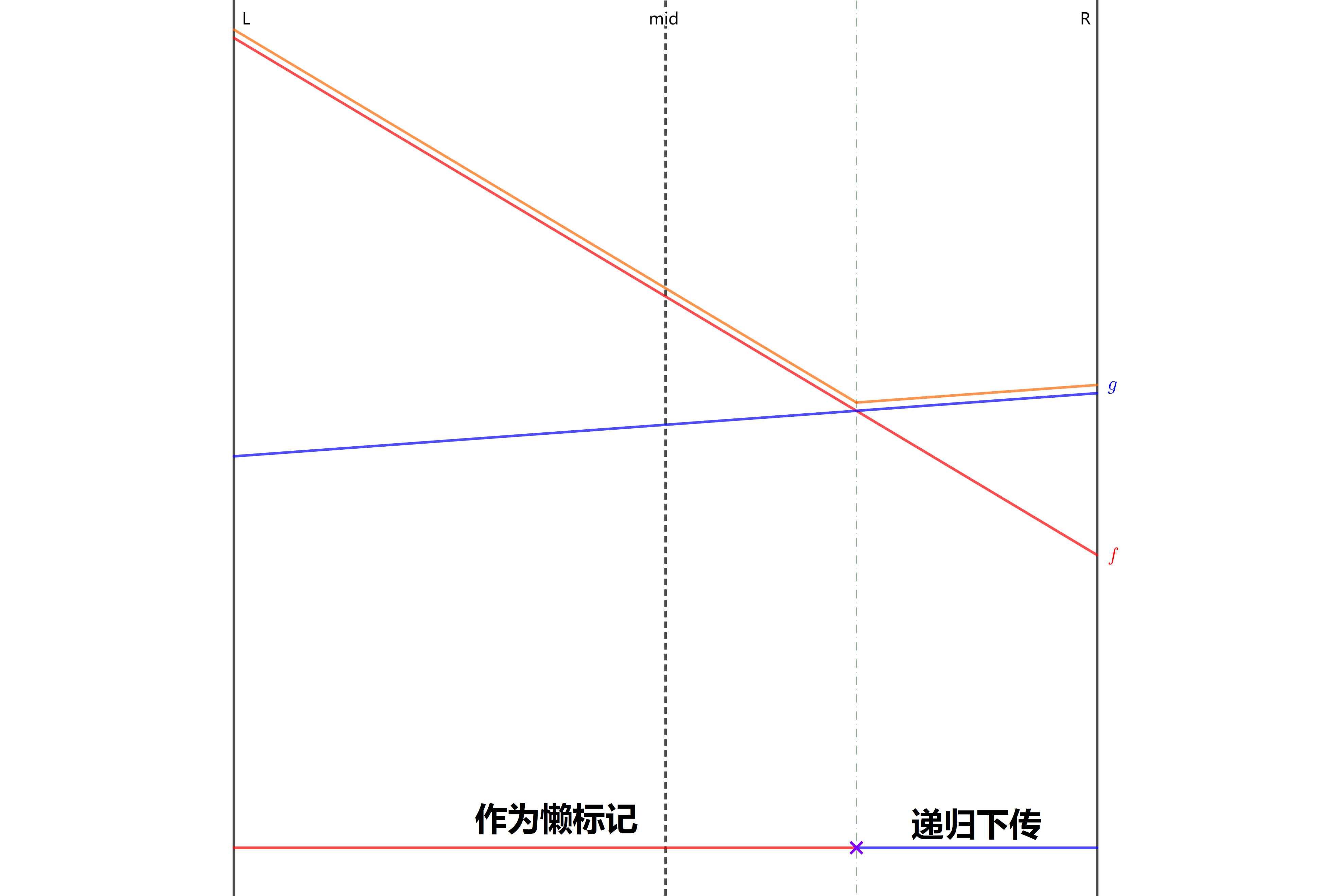
当 \(vl>ul\) 但是 \(vr<ur\) 时，那么说明线段 \(u,v\) 在 \([mid,r]\) 区间内肯定有交点。这时区间 \([l,mid]\) 的答案应该不变（但由于我们不知道 \(u,v\) 有没有交换过，所以我们还是修改一下。修改也很简单，对应区间修改的线段树，我们把 \([l,mid]\) 打上 tag），区间 \([mid,r]\) 我们应该递归下去。（如上图）

当 \(ul>vl\) 但是 \(vr>ur\) 时，那么说明线段 \(u,v\) 在 \([l,mid]\) 区间内肯定有交点。这时区间 \([mid,r]\) 的答案应该不变（但由于我们不知道 \(u,v\) 有没有交换过，所以我们还是修改一下。修改也很简单，对应区间修改的线段树，我们把 \([mid,r]\) 打上 tag），区间 \([l,mid]\) 我们应该递归下去。（如上图）

注意在讨论时我们要注意到在 \(x=mid\) 处 \(v\) 比 \(u\) 高这个大前提哈。

还有两种特殊情况，即有一个端点重合。那么我们就需要知道 \(u,v\) 有没有交换过了。我们考察下面的代码。

    if(bl==1||(!bl&&u<v))pushup(x<<1,l,mid,u);

我们把 !bl&&u<v 这种情况和 bl==1（即 \(ul>vl\)）的情况放在一起，因为我们知道新加入的线段的编号一定是大于之前的线段的编号的，所以如果 \(u<v\)，那么就说明 \(v\) 是新线段。如下。所以我们应该往左边的区间递归。

另外一种情况类似，请大家自己想一想吧！

那么现在 \(6\) 种情况我们都讨论过了，请仔细理解鸭。

查询¶

现在我们来看查询的部分。

pr query(int x,int l,int r,int q){
    if(q<l||q>r){
        return {0,0};
    }
    db res=cal(s[x],q);
    if(l==r)return {res,s[x]};
    int mid=(l+r)>>1;

    return pmax({res,s[x]},pmax(query(x<<1|1,mid+1,r,q),query(x<<1,l,mid,q)));
}

可以发现，这里和普通的线段树还是有一点区别的。这里的返回值是一个 pair<double,int> 分别是在 \(x=q\) 时的最高的线段的高度和线段的编号。

首先对于无解的情况，即询问的 \(x\) 在范围之外，我们直接返回最小值 \(-inf\) 或者 \(0\)（因为本题求最大值）即可，同时返回 \(id=0\) 表示不存在这条线段。

然后我们就需要计算当前这个节点对应的线段在 \(x=q\) 时的高度了，我们记为 \(res\)。假如 \(l=r\)，那么说明我们已经找到了叶子节点，直接返回 \(res\) 即可。但是如果这个点不是叶子节点，我们为什么还需要考虑当前节点的线段呢？直接递归下去不就行了？

注意！这里我们可没有 pushdown 操作！所以也许当前节点存储了新加入的高度更高的线段，但是叶子节点并没有更新！所以我们还需要采纳非叶子节点但也属于区间内的节点信息。当然，既然这个节点 \([l,r]\) 记录了这个线段，就说明再某个时刻这个区间内的最高点都在这个线段上，也就是说这个线段一定覆盖了这个区间，那么对于 \(x=q\) 也一定经过了这条线段。但是至于这条线段是否是最终答案我们暂时还不知道。总而言之，这条线段一定有成为答案的可能。

这里我们还需要引入一个辅助函数 pmax()。

pr pmax(pr a,pr b){//
    if(cmp(a.pf,b.pf)==-1)return b;
    if(cmp(a.pf,b.pf)==1)return a;
    if(a.ps<b.ps)return a;
    return b;
}

这个函数的功能是传入两个线段 \(a,b\)（注意这里传入的线段 \(a,b\) 为 pair<double,int> 类型，即已经计算好了当 \(x=q\) 时的高度值了，存放在 pair 的 .first 中），我们比较两个线段的 .first（代码中 define 为 pf），返回高的那个即可。请注意回顾 cmp 函数。

当然，题目要求“若有多条线段与查询直线的交点纵坐标都是最大的，则输出编号最小的线段”，所以就有了最后两行。

其他¶

现在线段树部分已经讲完了，我们最后考察加线段的函数（不是在线段树中，而是把线段加入 lne[] 数组中）。

void add(int x,int y,int a,int b){
    if(x==a){
        lne[++cnt].k=0,lne[cnt].b=max(y,b);
    }else{
        lne[++cnt].k=1.0*(b-y)/(a-x),lne[cnt].b=y-lne[cnt].k*x;
    }
}

这里线段的两个端点分别为 \((x,y)(a,b)\)，注意 \(x=a\) 的特殊情况。其他就是计算斜率和截距的常规操作了，初中知识即可。

代码¶

/*////////ACACACACACACAC///////////
       . Coding by Ntsc .
       . FancyKnowledge .
       . Prove Yourself .
/*////////ACACACACACACAC///////////

//头文件
#include<bits/stdc++.h>

//数据类型
#define int long long
#define ull unsigned long long
#define db double
#define endl '\n'
#define pr pair<double,int> 
#define pf first
#define ps second
//命名空间
using namespace std;
//常量
const int N=4e5+5;
const int M=1e3;
const int MOD=1e9+1;
const int INF=1e9;
const db eps=1e-9;
//变量
int n,m,a,b,c,s[N],y[N],lans,res,tmp,cnt,web[M][M];

struct line{
    db k,b;
}lne[N];

void add(int x,int y,int a,int b){
    if(x==a){
        lne[++cnt].k=0,lne[cnt].b=max(y,b);//why max?

    }else{
        lne[++cnt].k=1.0*(b-y)/(a-x),lne[cnt].b=y-lne[cnt].k*x;
    }
}

int cmp(double x, double y) {
  if (x-y>eps) return 1;
  if (y-x>eps) return -1;
  return 0;
}

db cal(int id,int p){//
    return 1.00*lne[id].b+p*lne[id].k;//计算直线id在x=p处的y
}

pr pmax(pr a,pr b){//
    if(cmp(a.pf,b.pf)==-1)return b;
    if(cmp(a.pf,b.pf)==1)return a;
    if(a.ps<b.ps)return a;
    return b;

}

void pushup(int x,int l,int r,int u){//ok
    int &v=s[x];
    int mid=(l+r)>>1,bmid=cmp(cal(u,mid),cal(v,mid));
    if(bmid==1||(!bmid&&u<v))swap(u,v);

    int bl=cmp(cal(u,l),cal(v,l));
    int br=cmp(cal(u,r),cal(v,r));

    if(bl==1||(!bl&&u<v))pushup(x<<1,l,mid,u);
    if(br==1||(!br&&u<v))pushup(x<<1|1,mid+1,r,u);


}


void change(int x,int l,int r,int ql,int qr,int v){//ok
    if(l>=ql&&r<=qr){
        pushup(x,l,r,v);return ;
    }
    int mid=(l+r)>>1;
    if(ql<=mid)change(x<<1,l,mid,ql,qr,v);
    if(qr>mid)change(x<<1|1,mid+1,r,ql,qr,v);
}


pr query(int x,int l,int r,int q){//ok
//  cerr<<"query l="<<l<<" r="<<r<<endl;
    if(q<l||q>r){
        return {0,0};
    }
    db res=cal(s[x],q);
    if(l==r)return {res,s[x]};
    int mid=(l+r)>>1;

    return pmax({res,s[x]},pmax(query(x<<1|1,mid+1,r,q),query(x<<1,l,mid,q)));
}


void solve(){
    scanf("%lld",&n);
    for(int i=1;i<=n;i++){
        int op,x,y,a,b,k;
        cin>>op;
        if(op){
            cin>>x>>y>>a>>b;
            x=(x+lans-1+39989)%39989+1;
            y=(y+lans-1+MOD)%MOD+1;//注意加上一个MOD
            a=(a+lans-1+39989)%39989+1;
            b=(b+lans-1+MOD)%MOD+1;
            if(x>a)swap(x,a),swap(y,b);
            add(x,y,a,b);
            change(1,1,39989,x,a,cnt);
        }else{
            cin>>k;

//          cerr<<"query k="<<(k+lans-1+39989)%39989+1<<endl;
            lans=query(1,1,39989,(k+lans-1+39989)%39989+1).ps;
            cout<<lans<<endl;
        }
    }
}

signed main(){
    int T;
    //  cin>>T;
    T=1;
    while(T--){
        solve();
    }

    return 0;
}

注意这是线段的情况，对于直线，我们把 change(1,1,39989,x,a,cnt); 中的 \(x,a\) 修改为询问的 \(x\) 的值域即可。原来的 \(x,a\) 为线段的两个端点的 \(x\) 值。

练习 #1 [JSOI2008] Blue Mary 开公司¶

第一行：一个整数 \(N\)，表示方案和询问的总数。

接下来 \(N\) 行，每行开头一个单词 Query 或 Project。

若单词为 Query，则后接一个整数 \(T\)，表示 Blue Mary 询问第 \(T\) 天的最大收益。

若单词为 Project，则后接两个实数 \(S, P\)，表示该种设计方案第一天的收益 \(S\)，以及以后每天比上一天多出的收益 \(P\)。

分析

本题即不断加入直线 \(y=S+P\times(x-1)\)，求对于某个 \(x\) 在所有直线中最高的 \(y\) 值为？

代码

/*////////ACACACACACACAC///////////
       . Coding by Ntsc .
       . FancyKnowledge .
       . Prove Yourself .
/*////////ACACACACACACAC///////////

//头文件
#include<bits/stdc++.h>

//数据类型
#define int long long
#define ull unsigned long long
#define db double
#define endl '\n'
#define pr pair<double,int> 
#define pf first
#define ps second
//命名空间
using namespace std;
//常量
const int N=4e5+5;
const int M=1e3;
const int MOD=1e9+1;
const int INF=1e9;
const int MT=5e4;
const db eps=1e-9;
//变量
int n,m,a,b,c,s[N],y[N],lans,res,tmp,cnt,web[M][M];

struct line{
    db k,b;
}lne[N];

void add(db s,db p){
    lne[++cnt].k=p,lne[cnt].b=s-p;

}

int cmp(double x, double y) {
  if (x-y>eps) return 1;
  if (y-x>eps) return -1;
  return 0;
}

db cal(int id,int p){//
    return 1.00*lne[id].b+p*lne[id].k;//计算直线id在x=p处的y
}

pr pmax(pr a,pr b){//
    if(cmp(a.pf,b.pf)==-1)return b;
    if(cmp(a.pf,b.pf)==1)return a;
    if(a.ps<b.ps)return a;
    return b;

}

void pushup(int x,int l,int r,int u){//ok
    int &v=s[x];
    int mid=(l+r)>>1,bmid=cmp(cal(u,mid),cal(v,mid));
    if(bmid==1||(!bmid&&u<v))swap(u,v);

    int bl=cmp(cal(u,l),cal(v,l));
    int br=cmp(cal(u,r),cal(v,r));

    if(bl==1||(!bl&&u<v))pushup(x<<1,l,mid,u);
    if(br==1||(!br&&u<v))pushup(x<<1|1,mid+1,r,u);


}


void change(int x,int l,int r,int ql,int qr,int v){//ok
    if(l>=ql&&r<=qr){
        pushup(x,l,r,v);return ;
    }
    int mid=(l+r)>>1;
    if(ql<=mid)change(x<<1,l,mid,ql,qr,v);
    if(qr>mid)change(x<<1|1,mid+1,r,ql,qr,v);
}


pr query(int x,int l,int r,int q){//ok
//  cerr<<"query l="<<l<<" r="<<r<<endl;
    if(q<l||q>r){
        return {0,0};
    }
    db res=cal(s[x],q);
    if(l==r)return {res,s[x]};
    int mid=(l+r)>>1;

    return pmax({res,s[x]},pmax(query(x<<1|1,mid+1,r,q),query(x<<1,l,mid,q)));
}


void solve(){
    scanf("%lld",&n);
    for(int i=1;i<=n;i++){
        string s;
        int T;
        db S,P;
        cin>>s;
        if(s=="Project"){
            cin>>S>>P;

            add(S,P);
            change(1,1,MT,1,MT,cnt);
        }else{
            cin>>T;
            lans=query(1,1,MT,T).pf;
            cout<<lans/100<<endl;
        }
    }
}

signed main(){
    solve();
    return 0;
}