manacher 马拉车算法¶

算法用途¶

给定一个字符串，然后输出这个字符串包含的最长回文子串。

普通算法的时间复杂度为$O(n^2)$，如下图

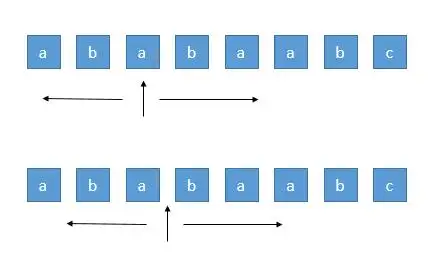
但manacher 算法的复杂度是$O(n)$，惊不惊喜意不意外！

算法实现¶

184 Manacher(马拉车)_哔哩哔哩_bilibili

改造字符串¶

初始化

在字符之间和串两端插入#，改造后都变成**奇回文串**，方便统一处理。

奇回文串 aba	#a#b#a#
偶回文串 abba	#a#b#b#a#

s[0] = '$' 是哨兵（边界）。

Code

void init(){
    scanf("%s",a+1);
//  scanf("%s",b+1);
    int n=strlen(a+1);
    s[0]='$';
    for(int i=1;i<=n;i++){
        s[++ls]='#',s[++ls]=a[i];
    }   
    s[++ls]='#';
}

优化数组

注释：d[i]记录长度的一半，向上取整（即$(len+1)\div 2$），即类似圆的半径，包含中间的那个字符

在“加速盒子”中，当枚举到点i=6时，加速盒子的区间变成$[i-d_i+1=3,i+d_i-1=9]$，当枚举到点$j(j>i,j<i+d_i-1)$时，d[j]就可以直接从$d[2\times i-j$]转移过来。但注意，对于边界的点$d[i+d_i-1=9]$不能直接转移，这个请看下面的分析。盒子外的暴力。

算法流程¶

计算完前i - 1个d函数，维护盒子[l,r]

如果i <= r(在盒内)，i的**对称点**为r-i+l， (1)若$d[r-i+l]\leq r-i+1$，则$d[i]=d[i-l+1]$。 (2)若$d[r-i+l]\geq r-i+1$，则令$d[i]=r-i+1$,从r+1往后暴力枚举。
如果i > r(在盒外)，则从i开始暴力枚举。
求出d[i]后，如果$i+d[i]-1>r$，则更新盒子$l=i-d[i]+1,r=l+d[i]-1$

情况

情况1：$i+d[r-i+l]≤r$时

我们盒子内的情况已知，所以可以安心地转移$d[i]=d[r-i+l]$

情况2：$i+d[r-i+l]>r$时

由于直接转移过来后以i为中心的回文串（图中i下方的蓝色长条）延申出了盒子，但是我们不知道盒子左右两侧的字符串是否也对称（即我们不知道盒子右边的信息），所以对于延申出盒子的部分我们要慢慢枚举。也就是说d[i]=d[r-i+1]是保底的，但r后面的就需要一个个去枚举判定了。

求出d[i] 后，如果i回文串（我们就姑且这么称呼它）的右端点延申到了当前盒子外，那么就应该更新盒子的l,r了。

转移以下两幅图表达方式是等效的，作者可能在不经意间转换表达方式哦。

Code

void getd(){
    d[1]=1;
    int l,r=1;//r只要小于2即可,目的是让下面第一次循环在i<=r不成立
    for(int i=2;i<=ls;i++){
        if(i<=r)d[i]=min(d[r-i+l],r-i+1);//转移d[i]且判定是否超出r
        while(s[i-d[i]]==s[i+d[i]])d[i]++;//如果d[i]没有超出r,那么第一次while判定就不成立,该语句不会执行.如果i本来就在盒子外面,则上面一句话不会执行,直接到本句话开始暴力
        if(i+d[i]-1>r)l=i-d[i]+1,r=i+d[i]-1;//转移盒子
    }
}

各部分说明

该算法时间复杂度可以证明为$O(n)$，因为你考虑i+d[i]，如果i+d[i]>r，那么才会执行while，然后又会将r修改为i+d[i]，即每次while运行一次，就会让r向右移动一位，r从1往右移动，到n停止，就n次。也就是说到会执行while时，i+d[i]一定是递增的，所以i+d[i] 只会从1递增到n，一共n次。这里描述不当，请仔细体会。

答案在d[]数组中，经过计算，答案取$\max(d[i]-1)$即可

/*////////ACACACACACACAC///////////
       . Code  by  Ntsc .
       . Earn knowledge .
/*////////ACACACACACACAC///////////

#include<bits/stdc++.h>
#define int long long
#define db double
#define rtn return
using namespace std;

const int N=2e7+2e6+5;//注意两倍空间 
const int M=1e5;
const int Mod=1e5;
const int INF=1e5;

int n,m,p,q,T;
char s[N];
int ls,ans,d[N];
char a[N];

void init(){
    scanf("%s",a+1);
//  scanf("%s",b+1);
    n=strlen(a+1);
    s[0]='$';
    for(int i=1;i<=n;i++){
        s[++ls]='#',s[++ls]=a[i];
    }   
    s[++ls]='#';
}

void getd(){
    d[1]=1;
    int l,r=1;//r只要小于2即可,目的是让下面第一次循环在i<=r不成立
    for(int i=2;i<=ls;i++){
        if(i<=r)d[i]=min(d[r-i+l],r-i+1);//转移d[i]且判定是否超出r
        while(s[i-d[i]]==s[i+d[i]])d[i]++;//如果d[i]没有超出r,那么第一次while判定就不成立,该语句不会执行.如果i本来就在盒子外面,则上面一句话不会执行,直接到本句话开始暴力
        if(i+d[i]-1>r)l=i-d[i]+1,r=i+d[i]-1;//转移盒子
    }
}

signed main(){

    init();
    getd();

    for(int i=1;i<=ls;i++)ans=max(ans,d[i]-1); 
    cout<<ans<<endl;
    return 0;
}

例题 #1¶

Codeforces Round 934 (Div. 2) 6/7 D

如果至少存在一个长度为 $k$ 的子串 $^\dagger$ 不是回文 $^\ddagger$ ，则称字符串 $t$ 为 $k$ (-good)。让 $f(t)$ 表示所有 $k$ 的值之和，使得字符串 $t$ 是 $k$ -good。

给你一个长度为 $n$ 的字符串 $s$ 。您需要回答以下问题中的 $q$ 个：

给定 $l$ 和 $r$ ( $l<r$ ), 求 $f(s _ ls _ {l + 1}\ldots s _ r)$ 的值。

$^\dagger$ 字符串 $z$ 的子串是来自 $z$ 的连续字符段。例如，" $\mathtt{defor}$ "、" $\mathtt{code}$ "和" $\mathtt{o}$ "都是" $\mathtt{codeforces}$ "的子串，而" $\mathtt{codes}$ "和" $\mathtt{aaa}$ "不是。

$^\ddagger$ 回文字符串是指前后读法相同的字符串。例如，字符串" $\texttt{z}$ "、" $\texttt{aa}$ "和" $\texttt{tacocat}$ "是回文字符串，而" $\texttt{codeforces}$ "和" $\texttt{ab}$ "不是。

思路

想到了马拉车，但是没有想到逆向思维：考虑什么情况下这个子串不是k好的——那么就是这子串的所有长度为k的子串都是回文串。也想到了只有abab和aaaa的情况，但是没有思路实现。

事实上到了这一步就可以开始直接性质了，不是什么预处理，离线，也不是什么区间查询，就是性质。

我们考虑每一个k和字符串s是不是k好的串

首先s不可能是1好的串
如果k=n（s的长度），那么就要求s是一个回文串。否则s就是一个n好的串。
除此之外，如果k是奇数，那么就要求s是一个交替串，ababa。否则s就是一个k好的串。
如果k是偶数，那么就要求s只由一个字符组成。否则s就是一个k好的串。

那么怎么样快速判断呢？

预处理啊。首先对于k=n的情况，用马拉车算法处理一下每个点往两边扩展得到的最远的回文串即可。

对于判断s是不是只有一个字符，那么预处理时把原字符串按连续的相同字母拆分，编号，查询时看看头尾的编号是否相同即可。

对于判断s是不是交替串，那么可以记录位置i后面的哪一个位置开始不满足$s_i=s_{i+2}$。这个可以倒序扫一遍处理。

代码时间

#include <bits/stdc++.h>
#include <queue>
#define rep(l, r, i) for (int i = l, END##i = r; i <= END##i; ++i)
#define per(r, l, i) for (int i = r, END##i = l; i >= END##i; --i)
using namespace std;
#define pb push_back
#define mp make_pair
#define int long long
#define pii pair<int, int>
#define ps second
#define pf first

#define X(j) i[j]
#define Y(j) (dp[j] + (i[j] + L) * (i[j] + L))

#define rd read()
int read() {
  int xx = 0, ff = 1;
  char ch = getchar();
  while (ch < '0' || ch > '9') {
    if (ch == '-')
      ff = -1;
    ch = getchar();
  }
  while (ch >= '0' && ch <= '9')
    xx = xx * 10 + (ch - '0'), ch = getchar();
  return xx * ff;
}
void write(int out) {
  if (out < 0)
    putchar('-'), out = -out;
  if (out > 9)
    write(out / 10);
  putchar(out % 10 + '0');
}

const int N = 3e5 + 5;
const int INF = 1e18;

vector<int> manacher_odd(string s) {
    int n = s.size();
    s = "$" + s + "^";
    vector<int> p(n + 2);
    int l = 1, r = 1;
    for(int i = 1; i <= n; i++) {
        p[i] = max(0ll, min(r - i, p[l + (r - i)]));
        while(s[i - p[i]] == s[i + p[i]]) {
            p[i]++;
        }
        if(i + p[i] > r) {
            l = i - p[i], r = i + p[i];
        }
    }
    return vector<int>(begin(p) + 1, end(p) - 1);
}

vector<int> manacher(string s) {
    string t;
    for(auto c: s) {
        t += string("#") + c;
    }
    auto res = manacher_odd(t + "#");
    return vector<int>(begin(res) + 1, end(res) - 1);
}

#define int long long

void solve() 
{
    int n=rd, q=rd;

    string s; cin >> s;
    auto v = manacher(s);
    for (auto &x : v) x--;

    // we also need to know if all same, and all alternating 
    set <int> s1, s2;
    for (int i = 0; i < n - 1; i++){
        if (s[i] != s[i + 1]) s1.insert(i);
        if (i != n - 1 && s[i] != s[i + 2]) s2.insert(i);
    }

    while (q--){
        int l=rd-1, r=rd-1;
        if (l == r){
            cout << 0 << "\n";
            continue;
        }

        int len = r - l + 1;

        int ans=0;
        auto it = s1.lower_bound(l);
        if (it == s1.end() || (*it) >= r){
            ans = 0;
        } else {
            it = s2.lower_bound(l);
            if (it == s2.end() || (*it) >= r - 1){
                ans = ((len - 1)/ 2) * (((len - 1) / 2) + 1);
            } else {
                ans =  len * (len - 1) / 2 - 1;
            }
        }

        if (v[l + r] < (r - l + 1)) ans += len;

        cout << ans << "\n";
    }
}

signed main() {
  int T=rd;
  while(T--){
    solve();
  }
  return 0;
}

例题 #2 [国家集训队] 最长双回文串¶

题目描述

顺序和逆序读起来完全一样的串叫做回文串。比如 acbca 是回文串，而 abc 不是：abc 的顺序为 abc，逆序为 cba，不相同。

输入长度为 $n$ 的串 $S$，求 $S$ 的最长双回文子串 $T$，即可将 $T$ 分为两部分 $X, Y$（$|X|,|Y|≥1$）且 $X$ 和 $Y$ 都是回文串。

输入格式

一行由小写英文字母组成的字符串 $S$。

输出格式

一行一个整数，表示最长双回文子串的长度。

对于 $100\%$ 的数据，$2\leq |S|\leq 10^5$。

2018.12.10，2018.12.15：感谢 @Ycrpro 提供 hack 数据两组。

// Problem: P4555 [国家集训队] 最长双回文串
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4555
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Challenger: Erica N
// ----
#include<bits/stdc++.h>

using namespace std;
#define rd read()
#define ull unsigned long long
#define int long long 
#define itn int
#define ps second 
#define pf first

int  read(){
    int x;
    cin>>x;
    return x;
}
#define zerol = 1
#ifdef zerol
#define cdbg(x...) do { cerr << #x << " -> "; err(x); } while (0)
void err() {
    cerr << endl;
}
template<template<typename...> class T, typename t, typename... A>
void err(T<t> a, A... x) {
    for (auto v: a) cerr << v << ' ';
    err(x...);
}
template<typename T, typename... A>
void err(T a, A... x) {
    cerr << a << ' ';
    err(x...);
}
#else
#define dbg(...)
#endif
const int N=3e5+5;
const ull P=137;
const int INF=1e9+7;
/*

策略


*/

int n,m,p,q,T;
char s[N];
int ls,ans,d[N];
char a[N];

void init(){
    scanf("%s",a+1);
//  scanf("%s",b+1);
    n=strlen(a+1);
    s[0]='$';
    for(int i=1;i<=n;i++){
        s[++ls]='#',s[++ls]=a[i];
    }   
    s[++ls]='#';
}

void getd(){
    d[1]=1;
    int l,r=1;//r只要小于2即可,目的是让下面第一次循环在i<=r不成立
    for(int i=2;i<=ls;i++){
        if(i<=r)d[i]=min(d[r-i+l],r-i+1);//转移d[i]且判定是否超出r
        while(s[i-d[i]]==s[i+d[i]])d[i]++;//如果d[i]没有超出r,那么第一次while判定就不成立,该语句不会执行.如果i本来就在盒子外面,则上面一句话不会执行,直接到本句话开始暴力
        if(i+d[i]-1>r)l=i-d[i]+1,r=i+d[i]-1;//转移盒子
    }
}

int l[N],r[N];


signed main(){

    init();
    getd();

    for(int i=1;i<=ls;i++){
        l[i-d[i]+1]=max(l[i-d[i]+1],d[i]-1);
        r[i+d[i]-1]=max(r[i+d[i]-1],d[i]-1);
    }


    for(int i=1;i<=ls;i+=2){
        l[i]=max(l[i],l[i-2]-2);
    }

    for(int i=ls;i>=1;i-=2){
        r[i]=max(r[i],r[i+2]-2);
    }

    int ans=0;
    for(int i=1;i<=ls;i++){
        if(l[i]&&r[i])ans=max(ans,l[i]+r[i]);
    }
    cout<<ans<<endl;
    // cout<<ans<<endl;
    return 0;
}