哈希¶
哈希就是把一串独立的数字合并为一个数字。用最简单的哈希就是:
对一个仅含有0~9的序列进行哈希 那么当base取10时,就相当于把数字连起来。
例如:1 2 3 4 5的[3,5]区间的哈希值就是12345-12*1000=345
数值哈希¶
例题 #1 [USACO06DEC] Milk Patterns G¶
农夫 John 发现他的奶牛产奶的质量一直在变动。经过细致的调查,他发现:虽然他不能预见明天产奶的质量,但连续的若干天的质量有很多重叠。我们称之为一个“模式”。 John 的牛奶按质量可以被赋予一个 \(0\) 到 \(1000000\) 之间的数。并且 John 记录了 \(N\)(\(1 \le N \le 2 \times 10 ^ 4\))天的牛奶质量值。他想知道最长的出现了至少 \(K\)(\(2 \le K \le N\))次的模式的长度。比如 1 2 3 2 3 2 3 1 中 2 3 2 3 出现了两次。当 \(K = 2\) 时,这个长度为 \(4\)。
二分一下走过最长长度。然后扫一遍,用桶记录以下各个哈希值出现的次数。
/*
Keyblinds Guide
###################
@Ntsc 2024
- Ctrl+Alt+G then P : Enter luogu problem details
- Ctrl+Alt+B : Run all cases in CPH
- ctrl+D : choose this and dump to the next
- ctrl+Shift+L : choose all like this
- ctrl+K then ctrl+W: close all
*/
#include <bits/stdc++.h>
#include <queue>
using namespace std;
#define rep(i, l, r) for (int i = l, END##i = r; i <= END##i; ++i)
#define per(i, r, l) for (int i = r, END##i = l; i >= END##i; --i)
#define pb push_back
#define mp make_pair
#define ull unsigned long long
#define int long long
#define pii pair<int, int>
#define ps second
#define pf first
// #define innt int
// #define inr int
// #define mian main
// #define iont int
#define rd read()
int read(){
int xx = 0, ff = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
ff = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
xx = xx * 10 + (ch - '0'), ch = getchar();
return xx * ff;
}
void write(int out) {
if (out < 0)
putchar('-'), out = -out;
if (out > 9)
write(out / 10);
putchar(out % 10 + '0');
}
#define nl dbg('\n')
const char el='\n';
const bool enable_dbg = 1;
template <typename T,typename... Args>
void dbg(T s,Args... args) {
if constexpr (enable_dbg){
cerr << s << ' ';
if constexpr (sizeof...(Args))
dbg(args...);
}
}
#define cdbg(x) cerr<<#x<<" : "<<x<<endl;
const int N = 3e6 + 5;
const int INF = 1e18;
const int M = 1e7;
const int MOD = 998244353;
ull hs[N];
ull pw[N];
const ull P=1e7+7;
ull getHs(int l,int r){
// cerr<<l<<' '<<r<<' '<<hs[r]-hs[l-1]*pw[r-l+1]<<endl;
return hs[r]-hs[l-1]*pw[r-l+1];
}
map<ull,int > cnt;
int n;
int K;
int a[N];
bool check(int l){
// cdbg(l);
cnt.clear();
for(int i=1;i<=n-l+1;i++){
cnt[getHs(i,i+l-1)]++;
if(cnt[getHs(i,i+l-1)]==K){
return 1;
}
}
return 0;
}
signed main(){
n=rd,K=rd;
for(int i=1;i<=n;i++){
a[i]=rd;
}
pw[0]=1;
for(int i=1;i<=n;i++){
pw[i]=pw[i-1]*P;
}
hs[0]=0;
for(int i=1;i<=n;i++){
hs[i]=hs[i-1]*P+a[i];
}
int l=1,r=n;
int res=0;
while(l<=r){
int mid=l+r>>1;
if(check(mid))res=mid,l=mid+1;
else r=mid-1;
}
cout<<res<<endl;
return 0;
}
字符串哈希¶
应用于字符串匹配的哈希算法。
例题 #1 后缀数组¶
题目描述
后缀数组 (SA) 是一种重要的数据结构,通常使用倍增或者 DC3 算法实现,这超出了我们的讨论范围。
在本题中,我们希望使用快排、Hash 与二分实现一个简单的 \(O(n\log^2n)\) 的后缀数组求法。
详细地说,给定一个长度为 \(n\) 的字符串 \(S\)(下标 \(0 \sim n-1\)),我们可以用整数 \(k(0 \le k < n)\) 表示字符串 \(S\) 的后缀 \(S(k \sim n-1)\)。
把字符串 \(S\) 的所有后缀按照字典序排列,排名为 \(i\) 的后缀记为 SA[i]。
额外地,我们考虑排名为 \(i\) 的后缀与排名为 \(i-1\) 的后缀,把二者的最长公共前缀的长度记为 Height[i]。
我们的任务就是求出 SA 与 Height 这两个数组。
下面给出的代码同时可以作为线性哈希的模板。
/*
Keyblinds Guide
###################
@Ntsc 2024
- Ctrl+Alt+G then P : Enter luogu problem details
- Ctrl+Alt+B : Run all cases in CPH
- ctrl+D : choose this and dump to the next
- ctrl+Shift+L : choose all like this
- ctrl+K then ctrl+W: close all
- Alt+la/ra : move mouse to pre/nxt pos'
*/
#include <bits/stdc++.h>
#include <queue>
using namespace std;
#define rep(i, l, r) for (int i = l, END##i = r; i <= END##i; ++i)
#define per(i, r, l) for (int i = r, END##i = l; i >= END##i; --i)
#define pb push_back
#define mp make_pair
#define int long long
#define pii pair<int, int>
#define ps second
#define pf first
// #define innt int
#define itn int
// #define inr intw
// #define mian main
// #define iont int
#define rd read()
int read(){
int xx = 0, ff = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
ff = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
xx = xx * 10 + (ch - '0'), ch = getchar();
return xx * ff;
}
void write(int out) {
if (out < 0)
putchar('-'), out = -out;
if (out > 9)
write(out / 10);
putchar(out % 10 + '0');
}
#define ell dbg('\n')
const char el='\n';
const bool enable_dbg = 1;
template <typename T,typename... Args>
void dbg(T s,Args... args) {
if constexpr (enable_dbg){
cerr << s;
if(1)cerr<<' ';
if constexpr (sizeof...(Args))
dbg(args...);
}
}
#define zerol = 1
#ifdef zerol
#define cdbg(x...) do { cerr << #x << " -> "; err(x); } while (0)
void err() { cerr << endl; }
template<template<typename...> class T, typename t, typename... A>
void err(T<t> a, A... x) { for (auto v: a) cerr << v << ' '; err(x...); }
template<typename T, typename... A>
void err(T a, A... x) { cerr << a << ' '; err(x...); }
#else
#define dbg(...)
#endif
const int N = 3e5 + 5;
const int INF = 1e18;
const int M = 1e7;
const int MOD = 1e9 + 7;
typedef unsigned long long ull;
ull pw[N],hs[N];
ull base=1e9+7;
string s;
int SA[N];
int n;
ull getHash(int l,int r){
return hs[r]-hs[l-1]*pw[r-l+1];//自然溢出
}
int findPos(int a,int b){
int l=-1,r=min(n-a+1,n-b+1)+1;
while(l+1<r){
int mid=l+r>>1;
if(getHash(a,a+mid-1)==getHash(b,b+mid-1))l=mid;
else r=mid;
}
return l;
}
bool cmp(int a,int b){
int p=findPos(a,b);
return s[a+p]<s[b+p];
}
void solve(){
cin>>s;
n=s.size();
s=" "+s;
pw[0]=1;
for(int i=1;i<=n;i++){
SA[i]=i;
pw[i]=pw[i-1]*base;
hs[i]=hs[i-1]*base+s[i];
}
sort(SA+1,SA+n+1,cmp);
for(itn i=1;i<=n;i++){
cout<<SA[i]-1<<' ';
}
cout<<endl;
for(itn i=1;i<=n;i++){
cout<<findPos(SA[i],SA[i-1])<<' ';
}
}
signed main() {
// freopen(".in","r",stdin);
// freopen(".in","w",stdout);
int T=1;
while(T--){
solve();
}
return 0;
}
例题 #2 纸牌游戏¶


哈希快速找到两个序列第一个不相同的数字,重载运算符,丢进优先队列。
#pragma GCC optimize("O3")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
/*
Keyblinds Guide
###################
@Ntsc 2024
- Ctrl+Alt+G then P : Enter luogu problem details
- Ctrl+Alt+B : Run all cases in CPH
- ctrl+D : choose this and dump to the next
- ctrl+Shift+L : choose all like this
- ctrl+K then ctrl+W: close all
- Alt+la/ra : move mouse to pre/nxt pos'
*/
#include <bits/stdc++.h>
#include <queue>
using namespace std;
#define rep(i, l, r) for (int i = l, END##i = r; i <= END##i; ++i)
#define per(i, r, l) for (int i = r, END##i = l; i >= END##i; --i)
#define pb push_back
#define mp make_pair
// #define int long long
#define pii pair<int, int>
#define ps second
#define pf first
// #define innt int
#define itn int
// #define inr int
// #define mian main
// #define iont int
#define rd read()
int read() {
int xx = 0, ff = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
ff = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') xx = xx * 10 + (ch - '0'), ch = getchar();
return xx * ff;
}
void write(int out) {
if (out < 0)
putchar('-'), out = -out;
if (out > 9)
write(out / 10);
putchar(out % 10 + '0');
}
#define ell dbg('\n')
const char el = '\n';
const bool enable_dbg = 1;
template <typename T, typename... Args>
void dbg(T s, Args... args) {
if constexpr (enable_dbg) {
cerr << s;
if (1)
cerr << ' ';
if constexpr (sizeof...(Args))
dbg(args...);
}
}
#define zerol = 1
#ifdef zerol
#define cdbg(x...) \
do { \
cerr << #x << " -> "; \
err(x); \
} while (0)
void err() { cerr << endl; }
template <template <typename...> class T, typename t, typename... A>
void err(T<t> a, A... x) {
for (auto v : a) cerr << v << ' ';
err(x...);
}
template <typename T, typename... A>
void err(T a, A... x) {
cerr << a << ' ';
err(x...);
}
#else
#define dbg(...)
#endif
const int N = 3e3 + 5;
const int INF = 1e18;
const int M = 1e7;
const int MOD = 1e9 + 7;
// 贪心?
const int P = 99248247;
itn ksm(int a, itn b) {
int res = 1;
while (b) {
if (b & 1)
res = (res * a) % MOD;
b >>= 1;
a = (a * a) % MOD;
}
return res;
}
int pw[N];
struct node {
int l, cnt, a[1002];
int hs[1002];
void input() {
a[0] = 0;
l = rd;
for (int i = 1; i <= l; i++) {
a[i] = rd;
}
cnt = 0;
}
void initHash() {
for (int i = 1; i <= l + 1; i++) {
hs[i] = ((long long)hs[i - 1] * P%MOD + a[i - 1]) % MOD;
}
}
inline int calHash(int l, int r) const { return (hs[r + 1] - (long long)hs[l] * pw[r-l+1] % MOD + MOD) % MOD; }
bool operator<(const node &b) const {
// 加速这找的流程!
int L = 1, r = min(l - cnt, b.l - b.cnt); //长度
int len = min(l - cnt, b.l - b.cnt);
int res = -1; //相等?
while (L <= r) {
int mid = L + r >> 1;
if (calHash(1 + cnt, mid + cnt) == b.calHash(1 + b.cnt, mid + b.cnt))
L = mid + 1, res = L;
else
r = mid - 1;
}
if (calHash(1 + cnt, len + cnt) == b.calHash(1 + b.cnt, len + b.cnt)) {
return l - cnt < b.l - b.cnt;
}
return a[cnt + L] > b.a[L + b.cnt];
}
};
priority_queue<node> pq;
void solve() {
pw[0]=1;
for(itn i=1;i<=1002;i++)pw[i]=((long long)pw[i-1]*P)%MOD;
int n = rd;
for (int i = 1; i <= n; i++) {
node t;
t.input();
t.initHash();
pq.push(t);
}
// cdbg("---");
while (pq.size()) {
node cur = pq.top();
pq.pop();
write(cur.a[++cur.cnt]);
putchar(' ');
if (cur.cnt < cur.l)
pq.push(cur);
}
}
int a[N], b[N];
signed main() {
// freopen(".in","r",stdin);
// freopen(".in","w",stdout);
int T = 1;
while (T--) {
solve();
}
return 0;
}
双哈希防卡¶
专题 | 南外20230712-链表、哈希、并查集、分块 E题
例题 #1¶
给定两个长为 N 的数列 A,B 与 Q 次询问,每次询问给出 \(x_i,y_i\),求出A的前 \(x_i\) 项去重后是否与 B 的前 \(y_i\) 项相同。
题目的大意是要我们求出\(a\)的前\(i\)项的set与\(b\)的前\(j\)项的set是否相同。
首先最暴力的做法当然是把他们俩的set求出来,然后一一比对,这样肯定是不行的,所以我们寻求哈希的算法。
我们注意到,在之前志不畅哈希中,我们把每个字符映射成一个整数,那这样每一个字符串就会映射成一个整数,但是这样的话每个字母出现的顺序对哈希是有影响的。
但是在本题中我们**只关心这个字符是否出现过,而不关心它出现的顺序**。所以我们就不能使用之前字符串哈希的方法。
我们举个例子,字符串\(12\)和字符串\(21\)是不同的字符串,但是在两个set中先加入\(1\)再加入\(2\)和先加入\(2\)再加入\(1\),是一样的。
对于本题的哈希函数,我们很容易就可以想到加法,因为加法满足交换律,所以他对于顺序是没有要求的。
但是这样我们很轻松就可以举出反例,比如说\(1+2+6=2+3+4\)。那么我们就需要把这个哈希哈希函数变得复杂一点,比如说:
-
比对它们的和,平方的和,立方和分别是否相等
-
或者将每个数字左移若干位再右移若干位,再将它们相加比对它们是否相等。
-
我们也可以将每个数计算一个随机值出来:我们把每个数\(i\)分配一个随机数\(h_i\),将它的哈希值设定为\(i\times h_i\)
这个问题与树的同构较为相似。
ull shift(ull x){//ull是unsigned long long
x^=mask;//mask是随机质数
x^=x<<13;
x^=x>>7;
x^=x<<17
x^=mask;
return x;
}
上面就是一种哈希的算法,我们只需要保证一个建立一个\(x\)与其哈希值的单射即可。
总结一下对于这种顺序对结果没有影响的情况我们需要使用满足交换律的运算符来构建哈希函数,比如加法乘法或者异或。
我们维护一个前缀的哈希值。对于去重问题,我们在从前往后后加入数时,我们将它加入一个set中来判断是否之前已经存在过这个数,如果之前有过就不将它的哈希值算出进行累加。
Code
/*////////ACACACACACACAC///////////
. Coding by Ntsc .
. ToFind Chargcy .
. Prove Yourself .
/*////////ACACACACACACAC///////////
#include<bits/stdc++.h>
#define int long long
#define db double
#define rtn return
#define i1n int i=1;i<=n;i++
#define in1 int i=n;i>=1;i--
using namespace std;
const int N=2e5+5;
const int M=1e5;
const int Mod=1e5;
const int INF=1e5;
int suma[N],sumb[N],a[N],b[N],n,q,x,y,suma2[N],sumb2[N];
void solve(int x,int y){
if(suma[x]==sumb[y]&&suma2[x]==sumb2[y])cout<<"Yes\n";
else cout<<"No\n";
return;
}
int hashh(int x){
return x*x;
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++)cin>>b[i];
set<int> sa,sb;
for(int i=1;i<=n;i++){
suma[i]=suma[i-1];
suma2[i]=suma2[i-1];
sumb[i]=sumb[i-1];
sumb2[i]=sumb2[i-1];
if(sa.count(a[i])==0)
{
// cout<<"OK";
suma[i]+=hashh(a[i]);
suma2[i]+=a[i];
sa.insert(a[i]);
}
if(sb.count(b[i])==0){
sumb[i]+=hashh(b[i]);
sumb2[i]+=b[i];
sb.insert(b[i]);
}
}
cin>>q;
while(q--){
cin>>x>>y;
solve(x,y);
}
return 0;
}
SGT动态维护区间哈希¶
例题 #1 [JSOI2008] 火星人¶
题目描述
火星人最近研究了一种操作:求一个字串两个后缀的公共前缀。
比方说,有这样一个字符串:madamimadam,我们将这个字符串的各个字符予以标号:
```Plain Text 序号 1 2 3 4 5 6 7 8 9 10 11 字符 m a d a m i m a d a m
现在,火星人定义了一个函数 $LCQ(x, y)$,表示:该字符串中第 $x$ 个字符开始的字串,与该字符串中第 $y$ 个字符开始的字串,两个字串的公共前缀的长度。比方说,$LCQ(1, 7) = 5, LCQ(2, 10) = 1, LCQ(4, 7) = 0$
在研究 $LCQ$ 函数的过程中,火星人发现了这样的一个关联:如果把该字符串的所有后缀排好序,就可以很快地求出 $LCQ$ 函数的值;同样,如果求出了 $LCQ$ 函数的值,也可以很快地将该字符串的后缀排好序。
尽管火星人聪明地找到了求取 $LCQ$ 函数的快速算法,但不甘心认输的地球人又给火星人出了个难题:在求取 $LCQ$ 函数的同时,还可以改变字符串本身。具体地说,可以更改字符串中某一个字符的值,也可以在字符串中的某一个位置插入一个字符。地球人想考验一下,在如此复杂的问题中,火星人是否还能够做到很快地求取 $LCQ$ 函数的值。
输入格式
第一行给出初始的字符串。第二行是一个非负整数 $M$ ,表示操作的个数。接下来的M行,每行描述一个操作。操作有 $3$ 种,如下所示
1. 询问。语法:$Q$ $x$ $y$ ,$x$ ,$y$ 均为正整数。功能:计算 $LCQ(x,y)$ 限制:$1$ $\leq$ $x$ , $y$ $\leq$ 当前字符串长度 。
2. 修改。语法:$R$ $x$ $d$,$x$ 是正整数,$d$ 是字符。功能:将字符串中第 $x$ 个数修改为字符 $d$ 。限制:$x$ 不超过当前字符串长度。
3. 插入:语法:$I$ $x$ $d$ ,$x$ 是非负整数,$d$ 是字符。功能:在字符串第 $x$ 个字符之后插入字符 $d$ ,如果 $x=0$,则在字符串开头插入。限制:$x$ 不超过当前字符串长度
输出格式
对于输入文件中每一个询问操作,你都应该输出对应的答案。一个答案一行。
1. 所有字符串自始至终都只有小写字母构成。
2. $M\leq150,000$
3. 字符串长度L自始至终都满足$L\leq100,000$
4. 询问操作的个数不超过 $10,000$ 个。
对于第 $1$,$2$ 个数据,字符串长度自始至终都不超过 $1,000$
对于第 $3$,$4$,$5$ 个数据,没有插入操作。
2024/07/40 更新一组 hack。
---
暴力可过。下面代码没有参考价值。请参考 例题 #2
```C++
/*
Keyblinds Guide
###################
@Ntsc 2024
- Ctrl+Alt+G then P : Enter luogu problem details
- Ctrl+Alt+B : Run all cases in CPH
- ctrl+D : choose this and dump to the next
- ctrl+Shift+L : choose all like this
- ctrl+K then ctrl+W: close all
- Alt+la/ra : move mouse to pre/nxt pos'
*/
#include <bits/stdc++.h>
#include <queue>
using namespace std;
#define rep(i, l, r) for (int i = l, END##i = r; i <= END##i; ++i)
#define per(i, r, l) for (int i = r, END##i = l; i >= END##i; --i)
#define pb push_back
#define mp make_pair
#define int long long
#define ull unsigned long long
#define pii pair<int, int>
#define ps second
#define pf first
// #define innt int
#define itn int
// #define inr intw
// #define mian main
// #define iont int
#define rd read()
int read(){
int xx = 0, ff = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
ff = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
xx = xx * 10 + (ch - '0'), ch = getchar();
return xx * ff;
}
void write(int out) {
if (out < 0)
putchar('-'), out = -out;
if (out > 9)
write(out / 10);
putchar(out % 10 + '0');
}
#define ell dbg('\n')
const char el='\n';
const bool enable_dbg = 1;
template <typename T,typename... Args>
void dbg(T s,Args... args) {
if constexpr (enable_dbg){
cerr << s;
if(1)cerr<<' ';
if constexpr (sizeof...(Args))
dbg(args...);
}
}
#define zerol = 1
#ifdef zerol
#define cdbg(x...) do { cerr << #x << " -> "; err(x); } while (0)
void err() { cerr << endl; }
template<template<typename...> class T, typename t, typename... A>
void err(T<t> a, A... x) { for (auto v: a) cerr << v << ' '; err(x...); }
template<typename T, typename... A>
void err(T a, A... x) { cerr << a << ' '; err(x...); }
#else
#define dbg(...)
#endif
const int N = 3e5 + 5;
const int INF = 1e18;
const int M = 1e7;
const int MOD = 1e9 + 7;
string s;
void solve(){
cin>>s;
int m=rd;
while(m--){
char op;
cin>>op;
if(op=='Q'){
itn x=rd-1,y=rd-1;
int res=0;
while(s[x]==s[y]&&s[x]&&s[y]){
res++;
x++;
y++;
}
cout<<res<<endl;
}if(op=='R'){
int x=rd-1;
char c;
cin>>c;
s[x]=c;
}if(op=='I'){
int x=rd;
string c;
cin>>c;
s.insert(x,c);
}
}
}
signed main() {
// freopen(".in","r",stdin);
// freopen(".in","w",stdout);
int T=1;
while(T--){
solve();
}
return 0;
}
例题 #2¶


/*
Keyblinds Guide
###################
@Ntsc 2024
- Ctrl+Alt+G then P : Enter luogu problem details
- Ctrl+Alt+B : Run all cases in CPH
- ctrl+D : choose this and dump to the next
- ctrl+Shift+L : choose all like this
- ctrl+K then ctrl+W: close all
- Alt+la/ra : move mouse to pre/nxt pos'
*/
#include <bits/stdc++.h>
#include <queue>
using namespace std;
#define rep(i, l, r) for (int i = l, END##i = r; i <= END##i; ++i)
#define per(i, r, l) for (int i = r, END##i = l; i >= END##i; --i)
#define pb push_back
#define mp make_pair
#define int long long
#define pii pair<int, int>
#define ps second
#define pf first
#define ull unsigned long long
#define itn int
// #define inr int
// #define mian main
// #define iont int
#define rd read()
int read() {
int xx = 0, ff = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
ff = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') xx = xx * 10 + (ch - '0'), ch = getchar();
return xx * ff;
}
void write(int out) {
if (out < 0)
putchar('-'), out = -out;
if (out > 9)
write(out / 10);
putchar(out % 10 + '0');
}
#define ell dbg('\n')
const char el = '\n';
const bool enable_dbg = 1;
template <typename T, typename... Args>
void dbg(T s, Args... args) {
if constexpr (enable_dbg) {
cerr << s;
if (1)
cerr << ' ';
if constexpr (sizeof...(Args))
dbg(args...);
}
}
#define zerol = 1
#ifdef zerol
#define cdbg(x...) \
do { \
cerr << #x << " -> "; \
err(x); \
} while (0)
void err() { cerr << endl; }
template <template <typename...> class T, typename t, typename... A>
void err(T<t> a, A... x) {
for (auto v : a) cerr << v << ' ';
err(x...);
}
template <typename T, typename... A>
void err(T a, A... x) {
cerr << a << ' ';
err(x...);
}
#else
#define dbg(...)
#endif
const int N = 1e6 + 5;
const int INF = 1e18;
const int M = 1e7;
const int MOD = 1e9 + 7;
const int P = 1e2 + 7;
// const int P = 10;
ull pw[N];
namespace SGT {
struct node {
int sz, hs;
} t[N << 2];
void pushup(int x) {
t[x].sz = t[x << 1].sz + t[x << 1 | 1].sz;
t[x].hs = t[x << 1].hs * pw[t[x << 1 | 1].sz] + t[x << 1 | 1].hs;
// cdbg(x,t[x<<1|1].sz,t[x<<1].hs,t[x<<1|1].hs);
}
void changry(int x, int l, int r, int p, int v) {
// change&query
if (l == r) {
if (v > 0)
t[x].sz++;
else
t[x].sz--;
t[x].hs += v;
// cdbg(x,v,t[x].hs);
return;
}
int mid = l + r >> 1;
if (p <= mid)
changry(x << 1, l, mid, p, v);
else
changry(x << 1 | 1, mid + 1, r, p, v);
pushup(x);
}
} // namespace SGT
using namespace SGT;
int p[N], a[N];
int ans[N];
int top;
int b[N];
void solve() {
int n = rd, m = rd;
for (int i = 1; i <= n; i++) {
p[i] = rd;
}
for (int i = 1; i <= m; i++) {
b[i] = a[i] = rd;
}
sort(b + 1, b + m + 1);
// int len=unique(b+1,b+m+1)-b-1;
for (int i = 1; i <= m; i++) {
a[i] = lower_bound(b + 1, b + m + 1, a[i]) - b;
}
pw[0] = 1;
for (int i = 1; i <= m; i++) {
pw[i] = pw[i - 1] * P;
}
int hsp = 0, inp = 0;
for (int i = 0; i < n; i++) {
inp += pw[i];
}
for (int i = 1; i <= n; i++) {
hsp = hsp * P + p[i];
}
for (int i = 1; i <= n; i++) {
changry(1, 1, m, a[i], i);
}
// cdbg(1,t[1].hs);
if (t[1].hs == hsp) {
ans[++top] = 1;
}
for (int i = n + 1; i <= m; i++) {
hsp += inp;
changry(1, 1, m, a[i - n], -i + n);
changry(1, 1, m, a[i], i);
// cdbg(i-n+1,t[1].hs,hsp);
if (t[1].hs == hsp) {
ans[++top] = i - n + 1;
}
}
cout << top << endl;
for (int i = 1; i <= top; i++) {
cout << ans[i] << ' ';
}
}
signed main() {
// freopen(".in","r",stdin);
// freopen(".in","w",stdout);
int T = 1;
while (T--) {
solve();
}
return 0;
}
/*
3 4
2 3 1
2 4 1 3
*/
树哈希¶
专题 | 南外20230712-链表、哈希、并查集、分块 F题
例题 #1 [NOIP2018 普及组] 对称二叉树¶
一棵有点权的有根树如果满足以下条件,则被轩轩称为对称二叉树:
-
二叉树;
-
将这棵树所有节点的左右子树交换,新树和原树对应位置的结构相同且点权相等。
下图中节点内的数字为权值,节点外的 \(id\) 表示节点编号。
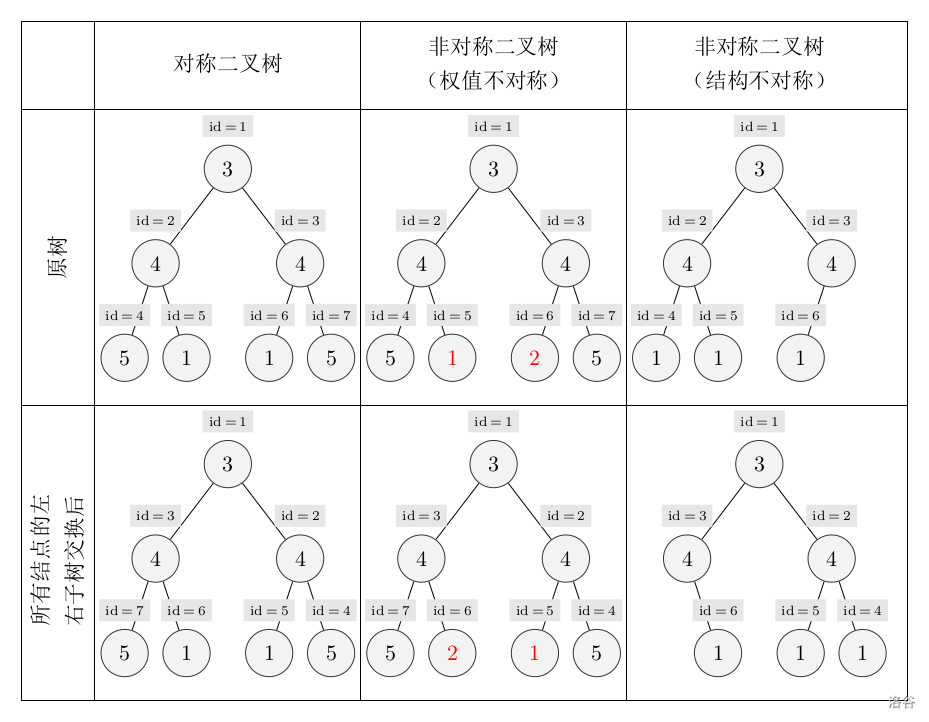
现在给出一棵二叉树,希望你找出它的一棵子树,该子树为对称二叉树,且节点数最多。请输出这棵子树的节点数。
注意:只有树根的树也是对称二叉树。本题中约定,以节点 \(T\) 为子树根的一棵“子 树”指的是:节点\(T\) 和它的全部后代节点构成的二叉树。
第一行一个正整数 \(n\),表示给定的树的节点的数目,规定节点编号 \(1 \sim n\),其中节点 \(1\) 是树根。
第二行 \(n\) 个正整数,用一个空格分隔,第 \(i\) 个正整数 \(v_i\) 代表节点 \(i\) 的权值。
接下来 \(n\) 行,每行两个正整数 \(l_i, r_i\),分别表示节点 \(i\) 的左右孩子的编号。如果不存在左 / 右孩子,则以 \(-1\) 表示。两个数之间用一个空格隔开。
\(v_i ≤ 1000\),\(n ≤ 10^6\)。
本题约定:
层次:节点的层次从根开始定义起,根为第一层,根的孩子为第二层。树中任一节 点的层次等于其父亲节点的层次加 \(1\)。
树的深度:树中节点的最大层次称为树的深度。
满二叉树:设二叉树的深度为 \(h\),且二叉树有 \(2^h-1\) 个节点,这就是满二叉树。
完全二叉树:设二叉树的深度为 \(h\),除第 \(h\) 层外,其它各层的结点数都达到最大 个数,第 \(h\) 层所有的结点都连续集中在最左边,这就是完全二叉树。

分别维护当前子树作为左子树和右子树的哈希值即可。为了防止卡哈希,我们要以不同的方式双哈希has1,has2
/*
CB Ntsc
*/
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define mp make_pair
#define rd read()
inline int read() {
int xx = 0, ff = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
ff = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') xx = xx * 10 + (ch - '0'), ch = getchar();
return xx * ff;
}
inline void write(int out) {
if (out < 0)
putchar('-'), out = -out;
if (out > 9)
write(out / 10);
putchar(out % 10 + '0');
}
const int N = 1e6 + 5;
const int M = 40;
const int INF = 1e9 + 5;
const int MOD = 9982353998244357;
const int MODD = 9982353998244357;
const int v1 = 998294353;
const int v2 = 998254357;
const int v3 = 988234357;
int v[N],has1l[N],has2l[N],has1r[N],has2r[N];
int sum[N],l[N],r[N];
int n,m,ans;
void pushup(int x){
has1l[x]=(has1l[l[x]]*v1+v[x]*v2+has1l[r[x]]*v3)%MOD;
has2l[x]=(has2l[l[x]]*v1+v[x]*v2+has2l[r[x]]*v3)%MODD;
has1r[x]=(has1r[r[x]]*v1+v[x]*v2+has1r[l[x]]*v3)%MOD;
has2r[x]=(has2r[r[x]]*v1+v[x]*v2+has2r[l[x]]*v3)%MODD;
}
void dfs(int x){
if(l[x])dfs(l[x]);
if(r[x])dfs(r[x]);
sum[x]=sum[l[x]]+sum[r[x]]+1;
if(sum[l[x]]==sum[r[x]]&&has1l[l[x]]==has1r[r[x]]&&has2l[l[x]]==has2r[r[x]])ans=max(ans,sum[x]);
pushup(x);
}
signed main(){
n=rd;
for(int i=1;i<=n;i++){
v[i]=rd;
}
for(int i=1;i<=n;i++){
l[i]=rd;r[i]=rd;
if(l[i]==-1)l[i]=0;
if(r[i]==-1)r[i]=0;
}
dfs(1);
cout<<ans<<endl;
return 0;
}
/*
1
2 5 1
0 0 1
0 0 4
*/
二维哈希¶
例题 #1 [BeiJing2011] Matrix 矩阵哈希¶
题目描述
给定一个 \(M\) 行 \(N\) 列的 \(01\) 矩阵,以及 \(Q\) 个 \(A\) 行 \(B\) 列的 \(01\) 矩阵,你需要求出这 \(Q\) 个矩阵哪些在原矩阵中出现过。
所谓 \(01\) 矩阵,就是矩阵中所有元素不是 \(0\) 就是 \(1\)。
输入格式
输入文件的第一行为 \(M,N,A,B\),参见题目描述。
接下来 \(M\) 行,每行 \(N\) 个字符,非 \(0\) 即 \(1\) ,描述原矩阵。
接下来一行为你要处理的询问数 \(Q\)。
接下来 \(Q\) 个矩阵,一共 \(Q\times A\) 行,每行 \(B\) 个字符,描述 \(Q\) 个 \(01\) 矩阵。
输出格式
你需要输出 \(Q\) 行,每行为 \(0\) 或者 \(1\),表示这个矩阵是否出现过,\(0\) 表示没有出现过,\(1\) 表示出现过。
对于 \(100\%\) 的实际测试数据,\(1\leq M,N \leq 1000\),\(Q = 1000\)。
对于 \(40\%\) 的数据,\(A = 1\)。
对于 \(80\%\) 的数据,\(A \leq 10\)。
对于 \(100\%\) 的数据,\(A \leq 100\)。
以下代码可以作为二维哈希的模板。
/*
Keyblinds Guide
###################
@Ntsc 2024
- Ctrl+Alt+G then P : Enter luogu problem details
- Ctrl+Alt+B : Run all cases in CPH
- ctrl+D : choose this and dump to the next
- ctrl+Shift+L : choose all like this
- ctrl+K then ctrl+W: close all
- Alt+la/ra : move mouse to pre/nxt pos'
*/
#include <bits/stdc++.h>
#include <queue>
using namespace std;
#define rep(i, l, r) for (int i = l, END##i = r; i <= END##i; ++i)
#define per(i, r, l) for (int i = r, END##i = l; i >= END##i; --i)
#define pb push_back
#define mp make_pair
#define int long long
#define pii pair<int, int>
#define ps second
#define pf first
// #define innt int
#define itn int
// #define inr intw
// #define mian main
// #define iont int
#define rd read()
int read(){
int xx = 0, ff = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
ff = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
xx = xx * 10 + (ch - '0'), ch = getchar();
return xx * ff;
}
void write(int out) {
if (out < 0)
putchar('-'), out = -out;
if (out > 9)
write(out / 10);
putchar(out % 10 + '0');
}
#define ull unsigned long long
#define ell dbg('\n')
const char el='\n';
const bool enable_dbg = 1;
template <typename T,typename... Args>
void dbg(T s,Args... args) {
if constexpr (enable_dbg){
cerr << s;
if(1)cerr<<' ';
if constexpr (sizeof...(Args))
dbg(args...);
}
}
#define zerol = 1
#ifdef zerol
#define cdbg(x...) do { cerr << #x << " -> "; err(x); } while (0)
void err() { cerr << endl; }
template<template<typename...> class T, typename t, typename... A>
void err(T<t> a, A... x) { for (auto v: a) cerr << v << ' '; err(x...); }
template<typename T, typename... A>
void err(T a, A... x) { cerr << a << ' '; err(x...); }
#else
#define dbg(...)
#endif
const int N = 3e3 + 5;
const int INF = 1e18;
const int M = 1e7;
const int P = 197;
const int P2 = 107;
ull f[N][N],g[N][N],G[N][N],F[N][N];
ull pw[N],pw2[N];
int a[N][N];
unordered_map<ull,bool> vis;
void solve(){
int n=rd,m=rd;
int A=rd,B=rd;
for(int i=1;i<=n;i++){
for(itn j=1;j<=m;j++){
char c;
cin>>c;
a[i][j]=c-'0';
}
}
pw[0]=pw2[0]=1;
for(int i=1;i<=max(n,m);i++){
pw[i]=pw[i-1]*P;
pw2[i]=pw2[i-1]*P2;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
f[i][j]=(f[i][j-1]*P+a[i][j]);
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
g[i][j]=(g[i-1][j]*P2+f[i][j]);
}
}
for(int i=A;i<=n;i++){
for(int j=B;j<=m;j++){
vis[g[i][j]-g[i-A][j]*pw2[A]-g[i][j-B]*pw[B]+g[i-A][j-B]*pw2[A]*pw[B]]=1;
}
}
itn q=rd;
while(q--){
for(int i=1;i<=A;i++){
for(int j=1;j<=B;j++){
char c;
cin>>c;
a[i][j]=c-'0';
}
}
for(int i=1;i<=A;i++){
for(int j=1;j<=B;j++){
F[i][j]=(F[i][j-1]*P+a[i][j]);
}
}
for(int i=1;i<=A;i++){
for(int j=1;j<=B;j++){
G[i][j]=(G[i-1][j]*P2+F[i][j]);
}
}
if(vis[G[A][B]]){
cout<<1<<endl;
}else{
cout<<0<<endl;
}
}
}
signed main() {
// freopen(".in","r",stdin);
// freopen(".in","w",stdout);
int T=1;
while(T--){
solve();
}
return 0;
}
例题 #2 [COCI2020-2021#3] Sateliti¶
题目描述
捕捉到的图像可以以一个 \(n \times m\) 的矩阵呈现,其中 * 表示火山,而 . 表示平地。我们认为两个图像属于同一颗卫星,当且它们能**环形地互相通过向上下或左右平移得到**。
科研工作者想要找到**字典序最小**的与给定图像属于同一颗卫星的图像。我们把图像的所有行依次连接组成字符串,再判断字符串的字典序即可。
输入格式
第一行包含两个整数 \(n,m\),表示图像的规模。
接下来的 \(n\) 行,每行输入 \(m\) 个字符,表示图像所对应的矩阵。
输出格式
输出共 \(n\) 行,每行有 \(m\) 个字符,表示满足要求的字典序最小的图像。
对于 \(100\%\) 的数据,\(1 \le n,m \le 1000\)。
【说明】
本题分值按 COCI 原题设置,满分 \(110\)。
题目译自 COCI2020-2021 CONTEST #3 T3 Sateliti。
大意
即给定一个字符矩阵,求在环形地上下左右平移后字典序最小的矩阵。对于矩阵的字典序,把矩阵的所有行依次连接组成字符串,再判断其字典序即可。
思路
因为我们可以进行环状的滚动,所以我们自然会把这个矩阵复制成4份分别放在左上,左下,右上,右下,这样我们就只需要在这个\(2n\times 2m\)的矩阵中截取一个字典序最小的矩阵即可。
那么我们怎么样截取字典序最小的矩阵呢?首先关注数据范围,我们是可以暴力枚举截取的矩阵的位置的(我们枚举截取的矩阵的左上角的坐标即可,因为要截取的矩阵的长宽是确定的,所以我们只要确定了左上角就可以确定这个被截取的矩阵)
可现在的问题是,我们花费了O(mn)是时间复杂度来枚举被截取的矩阵,那么我们肯定是要不断去把当前枚举到的矩阵的字典序c和前面的最优的字典序ans进行比较的。所以我们要考虑去怎么求出枚举的矩阵的字典序。
没有头绪?我们也许可以换一个角度思考。
如果我们要比较两个字符串的字典序是否相同,一种方法是求出他们的字典序,还有一种方法是**我们知道这两个字符串中第一个不同的位置,比较这两个位置上的字符的大小关系即可。**
如果是一个字符串,那么我们用第一张方法比较好,直接比较即可。但是现在我们是矩阵,我们使用第二种方法。
那么我们怎么样用第二种方法呢?这里我们需要使用**二维字符矩阵哈希**,总之就是一个快速判断两个区间是否相同的哈希,这里不再展开。
此时,我们要使用两个**二分**——第一个二分找到两个矩阵中第一个不相同的字符所出现的行,第二个二分我们在前面找到的行中找到那个最前面的不相同的地方。
这两个二分很明显是并列的而不是包含的。
本题核心:快速判断两个规模相同的矩阵的字典序。
实现:
我们需要快速求出一个矩阵的哈希值。我们可以考虑类似二维前缀和的写法来维护二维哈希
那么怎么样构建我们的二维哈希呢?先从一维开始:
一维情况下的数字哈希,我们取10作为P时,一个序列的哈希值就是其数值。那么一个数字矩形呢?我们可以把10的行宽次方作为行之间的Q,这样的哈希值就是数字串首尾相连得到的数值了。
那么我们就可以将P,Q用两个不同的质数替代。
代码
// Memory Limit: 0 MB
// Time Limit: 3000 ms
// Challenger: Erica N
// ----
#include<bits/stdc++.h>
using namespace std;
#define rd read()
#define ull unsigned long long
#define int long long
#define itn int
#define ps second
#define pf first
#define zerol = 1
#ifdef zerol
#define cdbg(x...) do { cerr << #x << " -> "; err(x); } while (0)
void err() {
cerr << endl;
}
template<template<typename...> class T, typename t, typename... A>
void err(T<t> a, A... x) {
for (auto v: a) cerr << v << ' ';
err(x...);
}
template<typename T, typename... A>
void err(T a, A... x) {
cerr << a << ' ';
err(x...);
}
#else
#define dbg(...)
#endif
const int N=3e3+5;
const ull P=137;
const ull P2=237;
const int INF=1e9+7;
/*
策略
*/
int n, m;
char s[N][N];
ull pw[N][N], h[N][N];
ull has(int i, int j, int i2, int j2) {
return (h[i + i2][j + j2] - h[i][j + j2] - h[i + i2][j] + h[i][j]);
}
bool equal(int x, int y, int x2, int y2, int x3, int y3) {
return has(x, y, x3, y3) * pw[x2][y2] == has(x2, y2, x3, y3) * pw[x][y];
}
int tx = 0, ty = 0;
void check(int i,int j){
int l = 1, r = n, res = 0;
while (l <= r) {
int mid = l + r >> 1;
if (equal(tx, ty, i, j, mid, m)) res = mid, l = mid + 1;
else r = mid - 1;
}
l = 1, r = m;
int res2 = 0;
while (l <= r) {
int mid = l + r >> 1;
if (equal(tx, ty, i, j, res + 1, mid)) res2 = mid, l = mid + 1;
else r = mid - 1;
}
if (res == n && res2 == m)
return;
if (s[(i + res) % n][(j + res2) % m] < s[(tx + res) % n][(ty + res2) % m])
tx = i, ty = j;
}
signed main() {
// freopen("telescope.in","r",stdin);
// freopen("telescope.out","w",stdout);
scanf("%lld%lld", &n, &m);
for (int i = 0; i < n; i++) {
scanf("%s", s[i]);
}
for (int i = 0; i < n << 1; i++) {
for (int j = 0; j < m << 1; j++) {
if (i == 0 && j == 0)pw[i][j] = 1;
else if (j == 0)pw[i][j] = pw[i - 1][j] * P;
else pw[i][j] = pw[i][j - 1] * P2;
}
}
for (int i = 0; i < n << 1; i++) {
for (int j = 0; j < m << 1; j++) {
h[i + 1][j + 1] = h[i][j + 1] + h[i + 1][j] - h[i][j] + (s[i % n][j % m]=='.') * pw[i][j];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
check(i,j);
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
printf("%c", s[(i + tx) % n][(j + ty) % m]);
}
printf("\n");
}
}
哈希的性质¶
例题 #1 哈希的可叠加性[ROIR 2022 Day 1] 回文数组¶
有两个自然数数组 \(A = [a_1, a_2, \dots , a_n]\) 和 \(B = [b_1, b_2, \dots , b_m]\)。
对每个数组,随机地去掉一个可能为空的前缀和一个可能为空的后缀,使得剩下的数组部分长度相等。我们将得到的数组记作 \(A'\) 和 \(B'\),它们的长度为 \(k\)。然后,对这两个数组的相应元素求和,结果数组记作 \(C = [c_1, c_2, \dots , c_k]\)。
例如,假设 \(n = 5,A = [4, 3, 3, 2, 1],m = 6,B = [4, 1, 5, 1, 3, 2]\),从数组 \(A\) 中去掉第一个和最后一个元素,从数组 \(B\) 中去掉前三个元素,得到 \(A' = [3, 3, 2],B' = [1, 3, 2]\),它们的相应元素求和结果为 \(C = [4, 6, 4]\)。 假设 \(n = 7,A = [1,9,1,9,8,1,0],m = 6,B = [1,1,4,5,1,4]\),从数组 \(A\) 中去掉前两个元素和最后一个元素,从数组 \(B\) 中去掉第一个和最后一个元素,得到 \(A' = [1,9,8,1],B' = [1,4,5,1]\),它们的相应元素求和结果为 \(C = [2,13,13,2]\)。
题目描述
找到能够得到回文数组 \(C\) 的最大长度 \(k\)。
输入格式
第一行输入两个整数 \(n\) 和 \(m\),分别表示第一个数组和第二个数组的元素数量 (\(1 \le n, m \le 100 000\))。
第二行输入 \(n\) 个整数 \(a_1,a_2,\dots,a_n\),表示数组 \(A\)(\(1 \le a_i \le 100\))。
第三行输入 \(m\) 个整数 \(b_1,b_2,\dots,b_n\),表示数组 \(B\)(\(1 \le b_i \le 100\))。
输出格式
输出一个整数,表示能够得到的最长回文数组的长度 \(k\)。
考虑到base取>最大值域时,hs_{plus(a,b)}=hs_a+hs_b。其中plus(a,b)代表对于a,b,将a_i+b_i逐个相加后得到的新序列。