跳转至

线段树建图优化

线段树见图优化可以使得我们轻松应对类似“一个点向一个区间内的点连边”的问题。

例题 #1 Legacy

题面翻译

Rick 和他的同事们做出了一种新的带放射性的婴儿食品(???根据图片和原文的确如此...)，与此同时很多坏人正追赶着他们。因此 Rick 想在坏人们捉到他之前把他的遗产留给 Morty。

在宇宙中一共有 \(n\) 个星球标号为 \(1 \sim n\)。Rick 现在身处于标号为 \(s\) 的星球(地球)但是他不知道 Morty 在哪里。

众所周知，Rick 有一个传送枪，他用这把枪可以制造出一个从他所在的星球通往其他星球(也包括自己所在的星球)的单行道路。但是由于他还在用免费版，因此这把枪的使用是有限制的。

默认情况下他不能用这把枪开启任何传送门。在网络上有 \(q\) 个售卖这些传送枪的使用方案。每一次你想要实施这个方案时你都可以购买它，但是每次购买后只能使用一次。每个方案的购买次数都是无限的。

网络上一共有三种方案可供购买：

  • 开启一扇从星球 \(v\) 到星球 \(u\) 的传送门；

  • 开启一扇从星球 \(v\) 到标号在 \([l,r]\) 区间范围内任何一个星球的传送门。(即这扇传送门可以从一个星球出发通往多个星球)

  • 开启一扇从标号在 \([l,r]\) 区间范围内任何一个星球到星球 \(v\) 的传送门。(即这扇传送门可以从多个星球出发到达同一个星球)

Rick 并不知道 Morty 在哪儿，但是 Unity 将要通知他 Morty 的具体位置，并且他想要赶快找到通往所有星球的道路各一条并立刻出发。因此对于每一个星球(包括地球本身)他想要知道从地球到那个星球所需的最小钱数。

思路

这道题考察的是**建图技巧**，没错就是网络流的那个。喵。

我们考虑最后一定是跑最短路来求的，那么我们怎么样对应三个不同的方案呢？

最简单的方法自然是直接连边，但是这样的边数量会变得很恐怖，并且我们也知道操作2，3是可以一次费用连多条边的，那么我们怎么样把费用对应到边上去呢？

所以我们考虑一下图论建图。

我们看看，区间我们想到了什么？线段树！

我们可以用线段树的\(\log n\)个节点来代表一个区间。所以名我们连边直接连到那\(\log n\)个节点，然后我们让线段树上的边都0。那么这里为什么我们需要建两颗线段树呢？因为如果建在一棵树上，那么我们边权不就都是0了吗？那么我们就别做了。最后我们还要沟通两棵树之间的代表同一个点的叶子节点，边权为0.至于最简单的操作一，我们也是直接连接叶子节点。

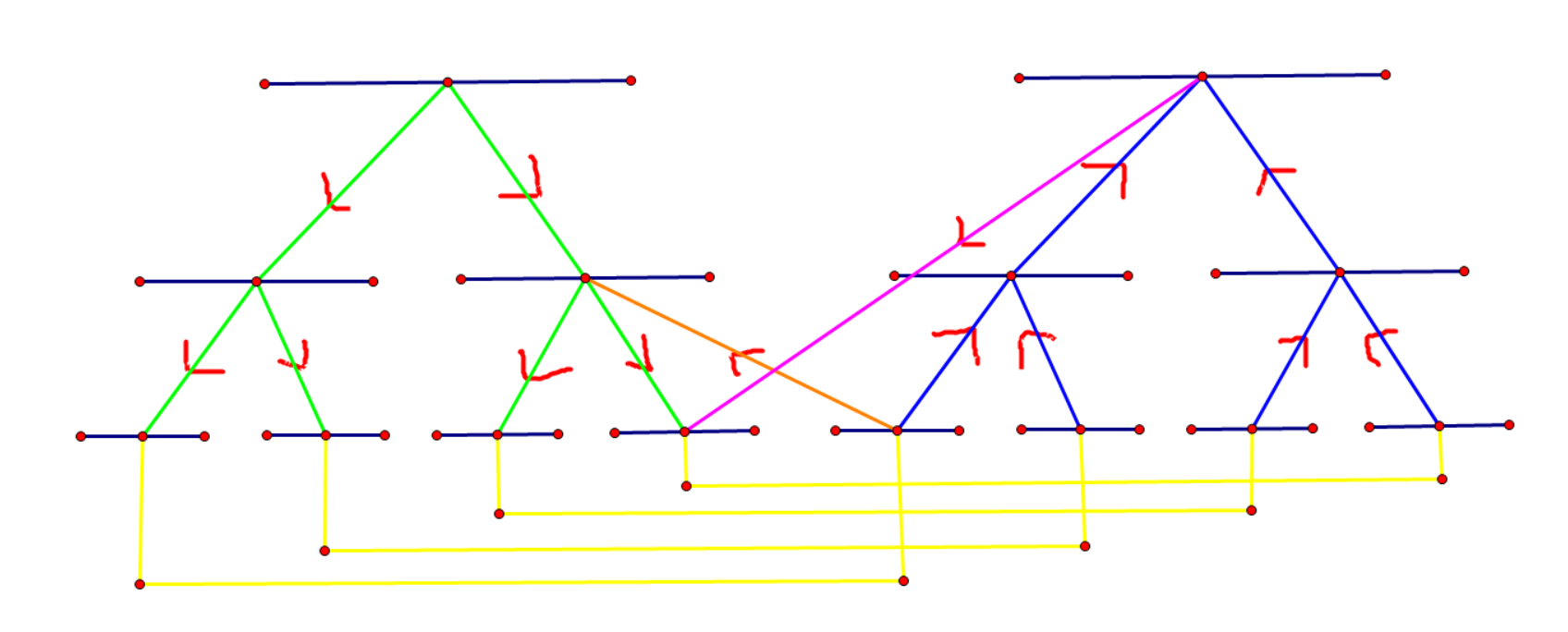
https://cdn.luogu.com.cn/upload/image_hosting/nciq2uft.png

好了，在建好图之后，我们跑最短路就行了。

代码

#include <bits/stdc++.h>
#include <queue>
using namespace std;

#define rep(i, l, r) for (int i = l, END##i = r; i <= END##i; ++i)
#define per(i, r, l) for (int i = r, END##i = l; i >= END##i; --i)
#define pb push_back
#define mp make_pair
#define int long long
#define pii pair<int, int>
#define ps second
#define pf first






#define rd read()
int read(){
    int xx = 0, ff = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        if (ch == '-')
            ff = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
      xx = xx * 10 + (ch - '0'), ch = getchar();
    return xx * ff;
}
void write(int out) {
    if (out < 0)
        putchar('-'), out = -out;
    if (out > 9)
        write(out / 10);
    putchar(out % 10 + '0');
}



const int N = 3e5 + 5;
const int INF = 1e18;
const int M = 1e6;
const int MOD = 1e9 + 7;


int n, m, s, cnt, root1, root2;
int head[M], lc[M], rc[M], tot;
struct edge {
    int v, w, nxt; 
}edge[N * 20];
inline void add(int u, int v, int w) { 
    edge[++tot].v = v, edge[tot].w = w, edge[tot].nxt = head[u]; head[u] = tot; 
}
void build_up(int &p,int l,int r) { 
    if (l == r) {
        p = l; 
        return;
    }
    p = ++cnt;  
    int mid = (l + r) >> 1;
    build_up(lc[p], l, mid);
    build_up(rc[p], mid + 1, r);
    add(p, lc[p], 0); 
    add(p, rc[p], 0); 
}
void build_down(int &p, int l, int r) { 
    if (l == r) { 
        p = l; 
        return;
    }
    p = ++cnt;
    int mid = (l + r) >> 1;
    build_down(lc[p], l, mid);
    build_down(rc[p], mid + 1, r);
    add(lc[p], p, 0); 
    add(rc[p], p, 0); 
}
int L, R;
void change(int p, int l, int r, int u, int w, int type) {
    if(L <= l && r <= R) { 
        type == 2 ? add(u, p, w) : add(p, u, w);
        return;
    }
    int mid = (l + r) >> 1;
    if (L <= mid) change(lc[p], l, mid, u, w, type);
    if (mid < R) change(rc[p], mid + 1, r, u, w, type);
}
int dis[M];
queue<int> Q;
void djstr(int s) { 
    memset(dis, 0x3F, sizeof dis);
    dis[s] = 0; Q.push(s);
    while(!Q.empty()) {
        int u = Q.front(); Q.pop();
        for(int i = head[u]; i; i = edge[i].nxt) {
            int v = edge[i].v, w = edge[i].w;
            if (dis[u] + w < dis[v]) 
                dis[v] = dis[u] + w,
                Q.push(v);
        }
    }
}
void solve() {
    n=rd,m=rd,s=rd;
    cnt = n; 
    build_up(root1, 1, n); 
    build_down(root2, 1, n);
    while (m--) {
        int op=rd, u, v, w;

        if(op == 1) {
            u=rd,v=rd,w=rd;
            add(u, v, w); 
        }
        else {
            u=rd,L=rd,R=rd,w=rd;
            change(op == 2 ? root1 : root2, 1, n, u, w, op);
        }
    }
    djstr(s);
    for(int i = 1; i <= n; i++) {
        if(dis[i] >= INF)dis[i] = -1;
        cout << dis[i] << " ";
    }
    return ;
}

signed main() {
    int T=1;
    while(T--){
        solve();
    }
    return 0;
}